题目内容
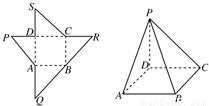
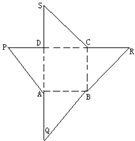 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要24
24
个这样的几何体,就可以拼成一个棱长为12的正方体.分析:先把判断几何体的形状,把展开图沿虚线折叠,得到一个四棱锥,求出体积,再计算棱长为12的正方体的体积,让正方体的体积除以四棱锥的体积,结果是几,就需要几个四棱锥.
解答:解: 把该几何体沿图中虚线将其折叠,使P,Q,R,S四点重合,所得几何体为下图中的四棱锥,
把该几何体沿图中虚线将其折叠,使P,Q,R,S四点重合,所得几何体为下图中的四棱锥,
且底面四边形ABCD为边长是6的正方形,侧棱PD⊥平面ABCD,PD=6
∴V四棱锥P-ABCD=
×6×6×6=72
∵棱长为12的正方体体积为12×12×12=1728
∵
=24,∴需要24个这样的几何体,就可以拼成一个棱长为12的正方体.
故答案为24
 把该几何体沿图中虚线将其折叠,使P,Q,R,S四点重合,所得几何体为下图中的四棱锥,
把该几何体沿图中虚线将其折叠,使P,Q,R,S四点重合,所得几何体为下图中的四棱锥,且底面四边形ABCD为边长是6的正方形,侧棱PD⊥平面ABCD,PD=6
∴V四棱锥P-ABCD=
| 1 |
| 3 |
∵棱长为12的正方体体积为12×12×12=1728
∵
| 1728 |
| 72 |
故答案为24
点评:本题主要考查了根据空间几何体的展开图判断原几何体形状,以及几何体体积的计算,考查了学生的识图能力以及空间想象力.

练习册系列答案
相关题目
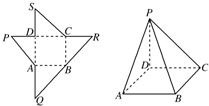 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要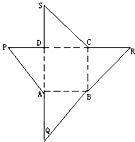 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为