题目内容
12.求下列函数的值域(1)y=3-$\frac{2}{x^2+2}$(2)y=2x-$\sqrt{x-2}$.
分析 (1)由题意得x2+2≥2,从而求函数的值域;
(2)化简y=2x-$\sqrt{x-2}$=2(x-2)-$\sqrt{x-2}$+4=2($\sqrt{x-2}$-$\frac{1}{4}$)2+$\frac{31}{8}$,从而求函数的值域.
解答 解:(1)∵x2+2≥2,
∴0<$\frac{2}{x^2+2}$≤1,
∴3-$\frac{2}{x^2+2}$∈[2,3);
故函数的值域为[2,3).
(2)∵y=2x-$\sqrt{x-2}$=2(x-2)-$\sqrt{x-2}$+4
=2($\sqrt{x-2}$-$\frac{1}{4}$)2+$\frac{31}{8}$,
∵($\sqrt{x-2}$-$\frac{1}{4}$)2≥0,
∴2($\sqrt{x-2}$-$\frac{1}{4}$)2+$\frac{31}{8}$≥$\frac{31}{8}$;
故函数的值域为[$\frac{31}{8}$,+∞).
点评 本题考查了函数的值域的求法.

练习册系列答案
相关题目
3.方程x3-3x+c=0恰有两个实数根,则c=( )
| A. | -2或2 | B. | -9或3 | C. | -1或1 | D. | -3或1 |
17.下面给出四个论断:①{0}是空集;②若a∈N,则-a∉N;③集合A={x∈R|x2-2x+1=0}有两个元素;④集合$B=\{x∈Q|\frac{6}{x}∈N\}$是有限集.其中正确的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),(x>0)}\\{{3}^{-x},(x≤0)}\end{array}\right.$,若f(m)>1,则实数m的取值范围是( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,1)∪(3,+∞) |
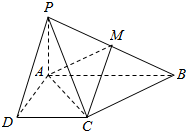 已知四棱锥P-ABCD的底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.