题目内容
17.下面给出四个论断:①{0}是空集;②若a∈N,则-a∉N;③集合A={x∈R|x2-2x+1=0}有两个元素;④集合$B=\{x∈Q|\frac{6}{x}∈N\}$是有限集.其中正确的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对四个选项分别进行判断,即可得出结论.
解答 解::①{0}中有元素0,不是空集,不正确;
②若a∈N,则-a∉N,不正确;
③集合A={x∈R|x2-2x+1=0}有1个元素1,不正确;
④集合$B=\{x∈Q|\frac{6}{x}∈N\}$是无限集,不正确.
故选:A.
点评 本题借助考查命题的真假判断,考查了自然数集的表示及集合中元素的性质,集合中元素性质:无序性、确定性、互异性.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.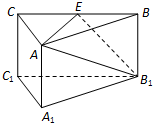 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AC⊥平面ABB1A1 | ||
| C. | A1C1∥平面AB1E | D. | AE,B1C1为异面直线,且AE⊥B1C1 |
8.以下命题正确的个数是( )
①命题“?x∈R,sinx>0”的否定是“?x∈R,sinx≤0”.
②命题“若x2+x-12=0,则x=4”的逆否命题为“若x≠4,则x2+x-12≠0”.
③若p∧q为假命题,则p、q均为假命题.
①命题“?x∈R,sinx>0”的否定是“?x∈R,sinx≤0”.
②命题“若x2+x-12=0,则x=4”的逆否命题为“若x≠4,则x2+x-12≠0”.
③若p∧q为假命题,则p、q均为假命题.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.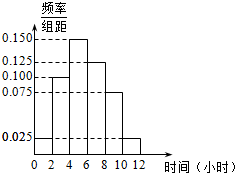 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图示),在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图示),在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
2.已知-个三棱锥与一个四棱锥,它们的所有棱为1,将三棱锥与四棱锥的侧面粘在一起使之完全重合,则所得到的多面体是( )
| A. | 五面体 | B. | 六面体 | C. | 七面体 | D. | 八面体 |
7.过平面外一点作平面的垂线可以作( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 无数条 |