题目内容
9.将下列各式化为Asin(α+φ)或Acos(α+φ)的形式:(1)5sinα-12cosα;
(2)$\frac{\sqrt{2}}{2}$cosα-$\frac{\sqrt{6}}{2}$sinα;
(3)-$\frac{\sqrt{3}}{3}$sinα-cosα.
分析 利用辅助角公式,易将其化为正弦型h或余弦型函数的形式.
解答 解:(1)5sinα-12cosα=13($\frac{5}{13}$sinα-$\frac{12}{13}$cosα)=13sin(α+φ),其中tanφ=$\frac{12}{5}$,
(2)$\frac{\sqrt{2}}{2}$cosα-$\frac{\sqrt{6}}{2}$sinα=$\sqrt{2}$($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα)=$\sqrt{2}$cos(α+$\frac{π}{3}$),
(3)-$\frac{\sqrt{3}}{3}$sinα-cosα=-$\frac{2\sqrt{3}}{3}$($\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα)=-$\frac{2\sqrt{3}}{3}$sin(α+$\frac{π}{3}$).
点评 在三角函数中,我们常用辅助角公式asinα+bcosα=$\sqrt{{a}^{2}+{b}^{2}}$sin(α+φ),将三角函数的表达式化为正弦型函数的形式

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.tan67°30′-tan22°30′的值为( )
| A. | 4 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
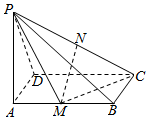 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.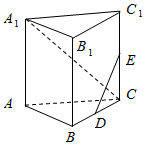 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.