题目内容
6.有8个面围成的几何体,每一个面都是正三角形,并且有四个顶点A,B,C,D在同一个平面内,ABCD是边长为30cm的正方形.(1)想象几何体的结构,并画出它的三视图和直观图;
(2)求出此积几何体的表面积和体积.
分析 (1)由题意画出几何体的直观图,进一步得到三视图;
(2)求出一个侧面正三角形的面积,乘以8求得几何体的侧面积,然后求出上部分正三棱锥的高,求得四棱锥的体积,乘以2得答案.
解答 解:(1)该几何体的三视图与直观图如图所示,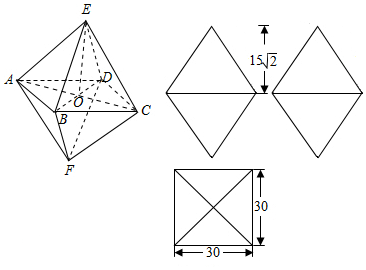
(2)这个是一个正八面体,假设另两个顶点为E,F,
ABCD是正方形,边长=30cm,
每个三角形面积是$\frac{1}{2}×30×15\sqrt{3}=225\sqrt{3}$,则表面积S=8×225$\sqrt{3}=2000\sqrt{3}$(cm2);
体积可以分成两部分,两部分是对称的四棱锥,连接AC,BD交于O,连接EO,
EO就是所要求的高,EO=15$\sqrt{2}$(cm),
半部分四棱锥体积是$\frac{1}{3}×30×30×15\sqrt{2}=4500\sqrt{2}$(cm3),总体积=9000$\sqrt{2}$(cm3).
点评 本题考查柱、锥、台体的体积,考查空间几何体的三视图和直观图,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
11.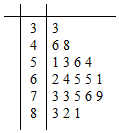 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
(Ⅱ) 根据列联表数据判断:能否在犯错的概率不超过5%的前提下,认为“满意与否”与“性别”有关?
附:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
附:
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
15.若等差数列{an}满足a8+a9+a10>0,a9+a10<0,则当n=( )时,{an}的前n项和最大.
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
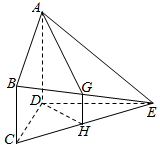 已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.
已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点. 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°. 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.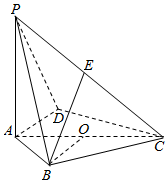 如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB
如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB