题目内容
1.若$\int\begin{array}{l}m\\ 1\end{array}$(2x-1)dx=6,则二项式(1-2x)3m的展开式各项系数和为-1.分析 由于$\int\begin{array}{l}m\\ 1\end{array}$(2x-1)dx=$({x}^{2}-x){|}_{1}^{m}$=6,化简解得m.令x=1,即可得出二项式(1-2x)3m展开式各项系数和.
解答 解:∵$\int\begin{array}{l}m\\ 1\end{array}$(2x-1)dx=$({x}^{2}-x){|}_{1}^{m}$=6,化为:m2-m-(1-1)=6,m>1,解得m=3.
令x=1,
则二项式(1-2x)3m即(1-2x)9展开式各项系数和=(1-2)9=-1.
故答案为:-1.
点评 本题考查了二项式定理的应用、微积分基本定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
13.在等比数列{an}中,设Sn为其前n项和,若a1a3=4,且S3=-3,则S4=( )
| A. | 31 | B. | -23 | C. | -5或$\frac{5}{2}$ | D. | 5或-$\frac{5}{2}$ |
 如图,已知四棱锥S-ABCD,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,E为线段AD的中点.
如图,已知四棱锥S-ABCD,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,E为线段AD的中点.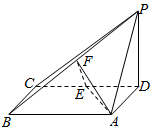 四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点. 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,E是BC的中点,现沿AD将平面PAD折起,使得PA⊥AB;
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,E是BC的中点,现沿AD将平面PAD折起,使得PA⊥AB;