题目内容
3.直线x+y-1=0被圆x2+y2-4x+6y+4=0截得的弦长为:2.分析 由圆的方程求出圆心和半径,求出圆心到直线x+y-1=0的距离d的值,再根据弦长公式求得弦长.
解答 解:圆x2+y2-4x+6y+4=0即(x-2)2+(y+3)2=9,表示以C(2,-3)为圆心,半径等于3的圆.
由于圆心到直线x+y-1=0的距离为d=$\frac{|2+3-1|}{\sqrt{2}}$=2$\sqrt{2}$,
故弦长为2$\sqrt{9-8}$=2,
故答案为:2.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.直线x+m2y+6=0与直线(m-2)x+3my+2m=0平行,则实数m的值为( )
| A. | m=0或m=3 | B. | m=-1或m=3 | C. | m=0或m=-1 | D. | m=-1 |
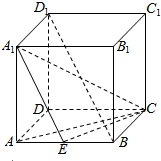 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.