题目内容
已知过抛物线y2=2px(p>0)的焦点❶,斜率为2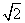 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.❷
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.❷
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,❸若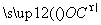 =
=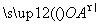 +λ
+λ ,求λ的值.
,求λ的值.
解 (1)直线AB的方程是y=2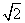
 ,与y2=2px联立,从而有4x2-5px+p2=0,所以x1+x2=
,与y2=2px联立,从而有4x2-5px+p2=0,所以x1+x2= ,
,
由抛物线定义得:|AB|=x1+x2+p= +p=9,
+p=9,
所以p=4,从而抛物线方程为y2=8x.
(2)由于p=4,4x2-5px+p2=0可简化为x2-5x+4=0,
从而x1=1,x2=4,y1=-2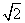 ,y2=4
,y2=4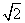 ,
,
从而A(1,-2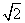 ),B(4,4
),B(4,4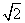 );
);
设C(x3,y3),则 =(x3,y3)=(1,-2
=(x3,y3)=(1,-2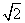 )+λ(4,4
)+λ(4,4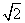 )=(4λ+1,4
)=(4λ+1,4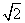 λ-2
λ-2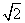 ),
),
又y =8x3,即[2
=8x3,即[2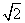 (2λ-1)]2=8(4λ+1),
(2λ-1)]2=8(4λ+1),
即(2λ-1)2=4λ+1,解得λ=0或λ=2.

练习册系列答案
相关题目
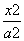 -
-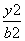 =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆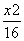 +
+ =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________.
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________.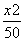 +
+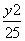 =1与圆M:x2+(y-5)2=9,双曲线G与椭圆D有相同焦点,它的两条渐近线恰好与圆M相切,求双曲线G的方程.
=1与圆M:x2+(y-5)2=9,双曲线G与椭圆D有相同焦点,它的两条渐近线恰好与圆M相切,求双曲线G的方程.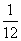 x2或y=-
x2或y=- x2
x2 是一个定值.
是一个定值.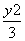 =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则 的最小值为( ).
的最小值为( ). C.1 D.0
C.1 D.0