题目内容
5.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 12 |
分析 由已知求得$|\overrightarrow{a}|$及$\overrightarrow{a}•\overrightarrow{b}$,再求出$|\overrightarrow{a}-2\overrightarrow{b}{|}^{2}$得答案.
解答 解:由$\overrightarrow{a}$=(2,0),得$|\overrightarrow{a}|=2$,
又|$\overrightarrow{b}$|=1,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°=2×1×(-\frac{1}{2})=-1$,
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}}=\sqrt{4+4+4}=2\sqrt{3}$,
故选:B.
点评 本题考查平面向量的数量积运算,考查了计算能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.设P(x,y)满足$\left\{\begin{array}{l}{x-2y≥0}\\{x+2y≥0}\end{array}\right.$,且P点到两直线x-2y=0,x+2y=0距离之和不大于$\sqrt{5}$,则x-y的最大值为( )
| A. | $\frac{17}{3}$ | B. | $\frac{15}{4}$ | C. | $\frac{25}{4}$ | D. | $\frac{11}{3}$ |
10.设集合M={x|x2≤4},N={x|log2x≤1},则M∩N=( )
| A. | [-2,2] | B. | {2} | C. | (0,2] | D. | (-∞,2] |
14.已知向量$\overrightarrow a=(2,-3),\overrightarrow b=(3,2)$,则$\overrightarrow a$与$\overrightarrow b$( )
| A. | 平行且同向 | B. | 垂直 | C. | 不垂直也不平行 | D. | 平行且反向 |
15.设向量$\overrightarrow{a}$=(-1,-2),$\overrightarrow{b}$=(m,m+1),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{b}$|等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{5}{9}$ | D. | 5 |
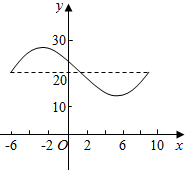 函数y=Asin(ωx+θ)+b的图象如图所示,则此函数的解析式为y=y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20.
函数y=Asin(ωx+θ)+b的图象如图所示,则此函数的解析式为y=y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20.