题目内容
12.已知数列{an}中,a1=1,其前n项和为Sn,且满足an=$\frac{{2S}_{n}^{2}}{2{S}_{n}-1}$(n≥2),则数列{an}的前n项和为Sn=$\frac{1}{2n-1}$.分析 an=$\frac{{2S}_{n}^{2}}{2{S}_{n}-1}$(n≥2),可得:(Sn-Sn-1)(2Sn-1)=2${S}_{n}^{2}$,化为$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,再利用等差数列的通项公式即可得出.
解答 解:∵an=$\frac{{2S}_{n}^{2}}{2{S}_{n}-1}$(n≥2),
∴(Sn-Sn-1)(2Sn-1)=2${S}_{n}^{2}$,
化为:-Sn-2SnSn-1+Sn-1=0,
∴$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,
∴数列$\{\frac{1}{{S}_{n}}\}$是等差数列,公差为2,首项为1.
∴$\frac{1}{{S}_{n}}$=1+2(n-1)=2n-1.
∴Sn=$\frac{1}{2n-1}$(n=1时也成立).
故答案为:$\frac{1}{2n-1}$.
点评 本题考查了递推关系、等差数列递通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.(2x2+3x+1)6的展开式中,x2的系数是( )
| A. | 72 | B. | 147 | C. | 132 | D. | 75 |
7.设向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x,4),则x=-2是$\overrightarrow{a}$∥$\overrightarrow{b}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.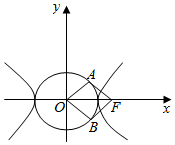 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
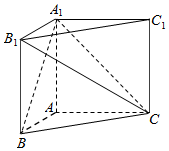 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.