题目内容
已知函数f(x)=x3-ax在区间〔1,+∞〕内是单调函数,则a的最大值是( )
| A、3 | B、2 | C、2 | D、0 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:对于函数f(x)=x3-ax,首先求出函数的导数,然后根据导数与函数单调性的关系进行判断.
解答:
解:f′(x)=3x2-a,
∵函数f(x)=x3-ax在(1,+∞)上是单调增函数,
∴在(1,+∞)上,f′(x)>0恒成立,
即a<3x2在(1,+∞)上恒成立,
∴a≤3,
故选:A.
∵函数f(x)=x3-ax在(1,+∞)上是单调增函数,
∴在(1,+∞)上,f′(x)>0恒成立,
即a<3x2在(1,+∞)上恒成立,
∴a≤3,
故选:A.
点评:本小题主要考查函数单调性的应用、函数导数与函数单调性之间的关系、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从1,2,3,…,20这20个正整数中,每次取3个不同的数组成等比数列,则不同等比数列的个数共有( )
| A、10 | B、16 | C、20 | D、22 |
从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,则这个数能被3整除的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0),过双曲线的一个焦点作实轴的垂线交双曲线于A、B两点,若
•
=0(O为坐标原点),则双曲线的离心率e等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
函数f(a)=(3m-1)a+b-2m,当m∈[0,1]时,0≤f(a)≤1恒成立,则
的最大值是( )
| b2-a2 |
| ab |
A、
| ||
| B、4 | ||
C、
| ||
| D、5 |
已知y=f(x)满足xf′(x)>-f(x)在R上恒成立,且a>b,则( )
| A、af(b)>bf(a) |
| B、af(a)>bf(b) |
| C、af(a)<bf(b) |
| D、af(b)<bf(a) |
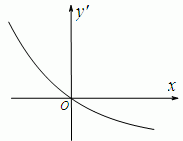 已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=
已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=