题目内容
8.已知三棱锥V-ABC的底面ABC是边长为4的正三角形,侧棱长都相等,其外接球(三棱锥的每个顶点都在球面上)的球心为O,满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{VO}$,则球O的体积为8$\sqrt{6}$π.分析 利用向量关系,得出∠AOB=∠VOC,从而△AOB≌△VOC,|VC|=|AB|=4,三棱锥V-ABC是棱长为4的正四面体,再利用勾股定理求出R,即可求出球O的体积.
解答 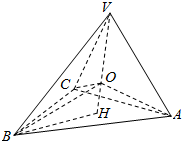 解:如图,设球O的半径为R,则|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=|$\overrightarrow{VO}$|=R.
解:如图,设球O的半径为R,则|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=|$\overrightarrow{VO}$|=R.
由$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{VO}$,可得$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{VO}$-$\overrightarrow{OC}$,
∴cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=cos<$\overrightarrow{OV}$,$\overrightarrow{OC}$>,
∴∠AOB=∠VOC,从而△AOB≌△VOC,
∴|VC|=|AB|=4,
∴三棱锥V-ABC是棱长为4的正四面体,
设V在△ABC中的射影为H,则|BH|=$\frac{4}{\sqrt{3}}$,|VH|=$\frac{4\sqrt{6}}{3}$,
Rt△OHB中,R2=($\frac{4}{\sqrt{3}}$)2+(R-$\frac{4\sqrt{6}}{3}$)2,∴R=$\sqrt{6}$,
∴V=8$\sqrt{6}$π.
故答案为:8$\sqrt{6}$π.
点评 本题考查球的体积,考查向量知识的运用,考查学生分析解决问题的能力,正确利用向量关系是关键.


| A. | 22+$\frac{2}{3}$π | B. | 22+$\frac{5}{3}$π | C. | 22+$\frac{8}{3}$π | D. | 22-π |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |