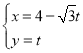题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交两点
相交两点![]() ,
,![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() ,
,![]() 的斜率之积为定值?若存在,求此圆的方程与定值;若不存在,请说明理由.
的斜率之积为定值?若存在,求此圆的方程与定值;若不存在,请说明理由.
【答案】(1)![]() ,(2)存在符合条件的圆,且此圆的方程为
,(2)存在符合条件的圆,且此圆的方程为![]() ,定值为
,定值为![]()
【解析】
(1)利用离心率和点在椭圆上列出方程,解出![]() 即可
即可
(2)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,先将直线的方程与椭圆的方程联立,利用直线
,先将直线的方程与椭圆的方程联立,利用直线![]() 与椭圆有且仅有一个公共点,推出
与椭圆有且仅有一个公共点,推出![]() ,然后通过直线与圆的方程联立,
,然后通过直线与圆的方程联立,
设![]() ,
,![]() ,结合韦达定理,求解直线的斜率乘积,推出
,结合韦达定理,求解直线的斜率乘积,推出![]() 为定值,然后再验证直线
为定值,然后再验证直线![]() 的斜率不存在时也满足即可
的斜率不存在时也满足即可
(1)由题意得:![]() ,
,![]()
又因为点![]() 在椭圆
在椭圆![]() 上
上
所以![]()
解得![]()
所以椭圆的标准方程为:![]()
(2)结论:存在符合条件的圆,且此圆的方程为![]()
证明如下:
假设存在符合条件的圆,且设此圆的方程为:![]()
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]()
由方程组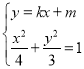 得
得![]()
因为直线![]() 与椭圆有且仅有一个公共点
与椭圆有且仅有一个公共点
所以![]()
即![]()
由方程组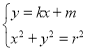 得
得![]()
则![]()
设![]() ,
,![]() ,则
,则![]()
设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]()
所以![]()
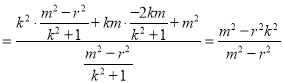
将![]() 代入上式得
代入上式得
![]()
要使得![]() 为定值,则
为定值,则![]() ,即
,即![]()
所以当圆的方程为![]() 时,
时,
圆与![]() 的交点
的交点![]() ,
,![]() 满足
满足![]() 为定值
为定值![]()
当直线![]() 的斜率不存在时,由题意知
的斜率不存在时,由题意知![]() 的方程为
的方程为![]()
此时圆与![]() 的交点
的交点![]() ,
,![]() 也满足
也满足![]() 为定值
为定值![]()
综上:当圆的方程为![]() 时,
时,
圆与![]() 的交点
的交点![]() ,
,![]() 满足
满足![]() 为定值
为定值![]()

【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?
【题目】下表是我省某地区2012年至2018年农村居民家庭年纯收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年纯收入 | 2 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2018年该地区农村居民家庭年纯收入的变化情况,并预测该地区2019年农村居民家庭年纯收入(结果精确到0.1)。
附:回归直线的斜率和截距的最小二乘法估计公式分别为: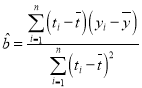 ,
,![]() 。
。