题目内容
(本小题共14分)已知函数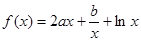 .
.
(Ⅰ)若函数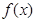 在
在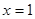 ,
,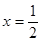 处取得极值,求
处取得极值,求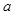 ,
,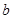 的值;
的值;
(Ⅱ)若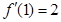 ,函数
,函数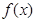 在
在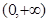 上是单调函数,求
上是单调函数,求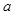 的取值范围.
的取值范围.
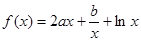 .
.(Ⅰ)若函数
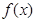 在
在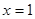 ,
,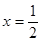 处取得极值,求
处取得极值,求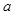 ,
,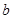 的值;
的值;(Ⅱ)若
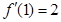 ,函数
,函数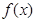 在
在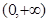 上是单调函数,求
上是单调函数,求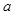 的取值范围.
的取值范围. 解:(Ⅰ) , ………………2分
, ………………2分
由 , ………………4分
, ………………4分
可得 . …………………6分
. …………………6分
(Ⅱ)函数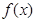 的定义域是
的定义域是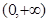 , ……………………7分
, ……………………7分
因为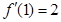 ,所以
,所以 . …………………8分
. …………………8分
所以 , ………………9分
, ………………9分
要使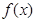 在
在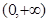 上是单调函数,只要
上是单调函数,只要 或
或 在
在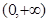 上恒成立.
上恒成立.
……………………10分
当 时,
时, 恒成立,所以
恒成立,所以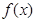 在
在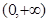 上是单调函数; ……11分
上是单调函数; ……11分
当 时,令
时,令 ,得
,得 ,
, ,
,
此时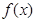 在
在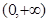 上不是单调函数; …………………12分
上不是单调函数; …………………12分
当 时,要使
时,要使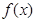 在
在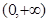 上是单调函数,只要
上是单调函数,只要 ,即
,即 .……13分
.……13分
综上所述,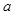 的取值范围是
的取值范围是 . …………………14分
. …………………14分
 , ………………2分
, ………………2分由
 , ………………4分
, ………………4分可得
 . …………………6分
. …………………6分(Ⅱ)函数
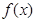 的定义域是
的定义域是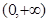 , ……………………7分
, ……………………7分因为
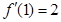 ,所以
,所以 . …………………8分
. …………………8分所以
 , ………………9分
, ………………9分要使
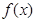 在
在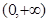 上是单调函数,只要
上是单调函数,只要 或
或 在
在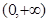 上恒成立.
上恒成立.……………………10分
当
 时,
时, 恒成立,所以
恒成立,所以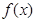 在
在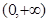 上是单调函数; ……11分
上是单调函数; ……11分当
 时,令
时,令 ,得
,得 ,
, ,
,此时
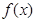 在
在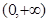 上不是单调函数; …………………12分
上不是单调函数; …………………12分当
 时,要使
时,要使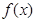 在
在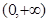 上是单调函数,只要
上是单调函数,只要 ,即
,即 .……13分
.……13分综上所述,
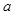 的取值范围是
的取值范围是 . …………………14分
. …………………14分略

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
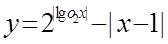 的图象大致是
的图象大致是 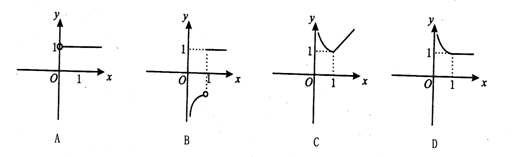
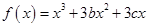 在两个极值点
在两个极值点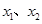 ,且
,且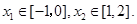 (1)求
(1)求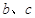 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点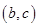 的区域;
的区域;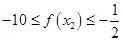
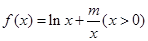 在
在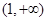 上为增函数,函数
上为增函数,函数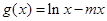
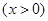 在
在 求出函数
求出函数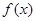 和
和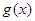 的导函数;
的导函数;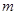 的值;
的值;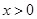 时,
时, 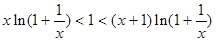
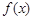 是定义在
是定义在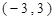 上的奇函数,当
上的奇函数,当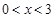 时,
时,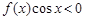 的解集是
的解集是 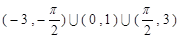
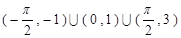
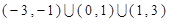
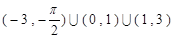
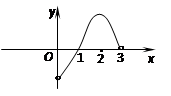
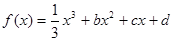 的图象过点
的图象过点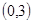 ,且在
,且在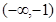 和
和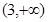 上为增函数,在
上为增函数,在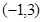 上为减函数.
上为减函数.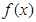 的解析式;
的解析式;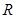 上的极值.
上的极值.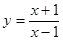 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线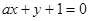 垂直,则
垂直,则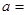
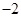
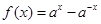
 在
在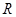 上是增函数,那么
上是增函数,那么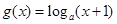 的大致图象是( )
的大致图象是( )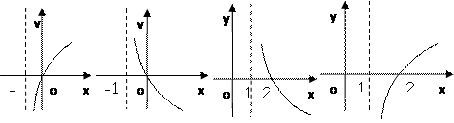
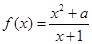 在
在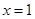 处取极值,则
处取极值,则