题目内容
已知二次函数 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行. (1)求
平行. (1)求 的解析式;(2)求函数
的解析式;(2)求函数 的单调递增区间及极值。(3)求函数
的单调递增区间及极值。(3)求函数 在
在 的最值。
的最值。
(1)由 ,可得
,可得 .
.
由题设可得 即
即
解得 ,
, .所以
.所以 .
.
(2)由题意得 ,
,
所以 .令
.令 ,得
,得 ,
, .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4/27 | 0 |
所以函数 的单调递增区间为
的单调递增区间为 ,
, .在
.在 有极小值为0。
有极小值为0。
在 有极大值4/27。
有极大值4/27。
(3)由 及(2),所以函数
及(2),所以函数 的最大值为2,最小值为0。.、
的最大值为2,最小值为0。.、

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目








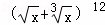 展开式中有理项共有 项.
展开式中有理项共有 项. ,集合A={
,集合A={ },B={
},B={ },若
},若 =R,则
=R,则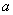 的取值范围为( )
的取值范围为( ) ,-2) B.(-
,-2) B.(-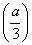 内单调递减,则a的取值范围是________.
内单调递减,则a的取值范围是________. 有且仅有一个正实数零点,则实数
有且仅有一个正实数零点,则实数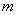 的取值范围是
的取值范围是 B.
B. C.
C. D.
D. ,则输入值
,则输入值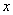 的取值范围为________.
的取值范围为________.
 B.
B.
 D.
D.

 在
在 上为减函数,则
上为减函数,则 的取值范围是 ( )A.
的取值范围是 ( )A. B.
B.  C.
C.  D.
D. 