题目内容
函数g(x)=ax3+2(1-a)x2-3ax在区间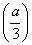 内单调递减,则a的取值范围是________.
内单调递减,则a的取值范围是________.
(-∞,-1]U{0}
【解析】 ∵g(x)在区间-∞, 内单调递减,
内单调递减,
∴g′(x)=3ax2+4(1-a)x-3a在 上的函数值非正,
上的函数值非正,
由于a<0,对称轴x= >0,故只需g′
>0,故只需g′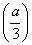 =
= +
+ a(1-a)-3a≤0,注意到a<0,
a(1-a)-3a≤0,注意到a<0,
∴a2+4(1-a)-9≥0,得a≤-1或a≥5(舍去).
故所求a的取值范围是(-∞,-1].

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 的图象向____平移 ____个单位长度就可得到函数y=sin2x的图象。
的图象向____平移 ____个单位长度就可得到函数y=sin2x的图象。 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )



 则 “
则 “ ”是“
”是“ ”的( )
”的( ) )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( ) ) B.[0,
) B.[0,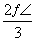 ,π) C.[
,π) C.[ 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行. (1)求
平行. (1)求 的解析式;(2)求函数
的解析式;(2)求函数 的单调递增区间及极值。(3)求函数
的单调递增区间及极值。(3)求函数 的最值。
的最值。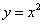 、
、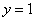 围成的区域的面积为
围成的区域的面积为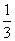 ; ② “
; ② “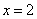 ”是“向量
”是“向量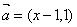 与向量
与向量 平行”的充分非必要条件; ③命题“
平行”的充分非必要条件; ③命题“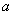 、
、 都是有理数”的否定是“
都是有理数”的否定是“ 的最小值等于
的最小值等于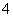 。其中正确结论的个数为
。其中正确结论的个数为 ( )
( ) B.
B. C.
C. D.
D.
 的最小值;
的最小值; ,且
,且 ,求
,求 的最大值.
的最大值.