题目内容
1．数列{an}满足an+1+（-1）nan=2n-1，则{an}的前80项和为（ ）| A． | 3690 | B． | 3660 | C． | 3240 | D． | 1830 |
分析 通过an+1+（-1）nan=2n-1计算可知从第一项开始依次取2个相邻奇数项的和都等于2、从第二项开始依次取2个相邻偶数项的和构成以8位首项、以16为公差的等差数列，进而计算可得结论．
解答 解：∵an+1+（-1）nan=2n-1，
∴a2-a1=1，a3+a2=3，a4-a3=5，a5+a4=7，…，a50-a49=97，
∴a3+a1=2，a4+a2=8，a7+a5=2，a8+a6=24，a9+a7=2，a12+a10=40，…
∴从第一项开始，依次取2个相邻奇数项的和都等于2；
从第二项开始，依次取2个相邻偶数项的和构成以8位首项、以16为公差的等差数列，
∴所求值为20×2+（20×8+$\frac{20×19}{2}$×16）=3240，
故选：C．
点评 本题考查数列的通项及前n项和，考查运算求解能力，对表达式的灵活变形是解决本题的关键，注意解题方法的积累，属于中档题．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
如图，椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{3}$，F，A分别是椭圆的左焦点和右点顶点，P是椭圆上任意一点，若$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值是12，则椭圆方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$．
6．已知复数z1=a+bi，z2=-1+ai（a，b∈R），若|z1|＜|z2|，则（ ）
| A． | b＜-1或b＞1 | B． | -1＜b＜1 | C． | b＞1 | D． | b＞0 |
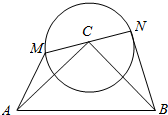Rt△ABC中，∠C=90°，AC=BC=2，⊙C的半径是1，MN是⊙C直径，求：$\overrightarrow{AM}$•$\overrightarrow{BN}$的最大值及此时$\overrightarrow{MN}$与$\overrightarrow{AB}$的关系．