题目内容
6.某人的一串钥匙有n把钥匙,其中只有一把能打开自己的家门,当他随意地试用这串钥匙时,求:打开门时已被试用过的钥匙数的数学期望与方差,假定.(1)把每次试用过的钥匙分开;
(2)把每次试用过的钥匙再混杂在这串钥匙中.
分析 (1)由已知得打开门时已被试用过的钥匙数X的可能取值为1,2,…,n,分别求出相应的概率,由此能求出打开门时已被试用过的钥匙数的数学期望与方差.
(2)由已知得打开门时已被试用过的钥匙数X的可能取值为1,2,…,n,分别求出相应的概率,由此能求出打开门时已被试用过的钥匙数的数学期望与方差.
解答 解:(1)由已知得打开门时已被试用过的钥匙数X的可能取值为1,2,…,n,
P(X=i)=$\frac{1}{n}$,i=0,1,2,…,n-1,
∴X的数学期望EX=(1+2+3+…+n)×$\frac{1}{n}$=$\frac{n+1}{2}$,
EX2=$\sum_{i=1}^{n}$i2$•\frac{1}{n}$=$\frac{(n+1)(2n+1)}{6}$,
∴X的方差为DX=EX2-(EX)2=$\frac{{n}^{2}-1}{12}$.
(2)由已知得打开门时已被试用过的钥匙数X的可能取值为1,2,…,n,
P(X=k)=($\frac{n-1}{n}$)k-1$•\frac{1}{n}$,k=1,2,…
EX=$\sum_{k=1}^{∞}$k•$(\frac{n-1}{n})^{k-1}$•$\frac{1}{n}$=n,
EX2=$\sum_{k=1}^{∞}{k}^{2}$•$(\frac{n-1}{n})^{k-1}$•$\frac{1}{n}$=2n2-n,
DX=(EX)2-EX2=n(n-1).
点评 本题考查离散型随机变量的数学期望与方差的求法,是中档题,解题时要认真审题,注意方差性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.函数y=log3|x|的图象大致形状是( )
| A. | 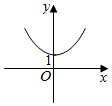 | B. |  | C. | 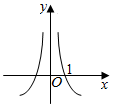 | D. | 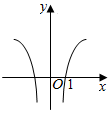 |
17.下列命题成立的是( )
| A. | 如果a>b,c≠0,那么$\frac{a}{c}>\frac{b}{c}$ | B. | 如果a>b,那么a2>b2 | ||
| C. | 如果a>b,c>d,那么a+d>b+c | D. | 如果a>b,c>d,那么a-d>b-c |
14.设函数f(x)=$\left\{\begin{array}{l}{2x+1,x>0}\\{0,x=0}\\{2x-1,x<0}\end{array}\right.$若不等式f(x-1)+f($\frac{m}{x}$)>0对任意x>0恒成立,则实数m的取值范围是( )
| A. | ($-\frac{1}{4}$,$\frac{1}{4}$) | B. | (0,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,+∞) | D. | (1,+∞) |
11.函数f(x)=2tan(-x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 奇函数,也是偶函数 | D. | 非奇非偶函数 |
16.不等式log2|2+x|≤1的解集为( )
| A. | {x|x≥0} | B. | {x|x≥-2} | C. | {x|0≤x≤1} | D. | {x|-4≤x≤0且x≠-2} |
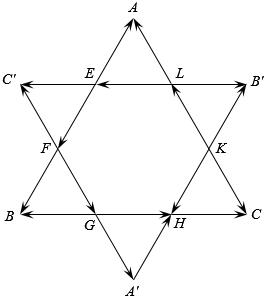 如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:
如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求: