题目内容
如图所示,有两条相交成60°角的直线xx′,yy′,交点为O,甲、乙分别在Ox、Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲眼xx′的方向、乙沿y′y的方向步行。求:

(Ⅰ)起初,两人的距离是多少?
(Ⅱ)用包含t的式子表示t小时后两人的距离;
(Ⅲ)什么时候两人的距离最短?
解:(Ⅰ)设甲、乙两人最初的位置是A、B,则

 ,
,
∴ (km)。
(km)。
(Ⅱ)设甲、乙两人t小时后的位置分别是P、Q,则 =4t,
=4t, =4t,
=4t,
当 时,
时, ,
,
当 时,
时, ,
,
注意到,上面两式实际上是统一的,所以 ,
,
即 。
。
(Ⅲ)∵ ,
,
∴当 时,即在第15分钟末,PQ最短,最短距离是2km。
时,即在第15分钟末,PQ最短,最短距离是2km。

 ,
,∴
 (km)。
(km)。(Ⅱ)设甲、乙两人t小时后的位置分别是P、Q,则
 =4t,
=4t, =4t,
=4t,当
 时,
时, ,
,当
 时,
时, ,
,注意到,上面两式实际上是统一的,所以
 ,
,即
 。
。(Ⅲ)∵
 ,
,∴当
 时,即在第15分钟末,PQ最短,最短距离是2km。
时,即在第15分钟末,PQ最短,最短距离是2km。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.
如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.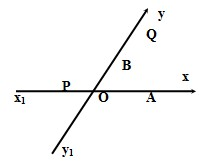 如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?
如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短? 如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.
如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.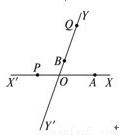
 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 km,乙离
km,乙离 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向步行.
的方向步行. 的式子表示
的式子表示