题目内容
 如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.
如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.(1)起初两车的距离是多少?
(2)t小时后两车的距离是多少?
(3)何时两车的距离最短?
分析:(1)先设甲、乙两车最初的位置为A、B,将距离转化为向量问题,然后利用向量的数量积运算求甲乙两车的距离.
(2)设甲、乙两车t小时后的位置分别为P、Q,则|
|=60t,|
|=60t.利用余弦定理可得即|
|=10
km.
(3)由(2)得关于PQ的表达式,通过利用二次函数可探讨其最大值.
(2)设甲、乙两车t小时后的位置分别为P、Q,则|
| AP |
| BQ |
| PQ |
| 108t2-36t+7 |
(3)由(2)得关于PQ的表达式,通过利用二次函数可探讨其最大值.
解答:解:(1)设甲、乙两车最初的位置为A、B,
则|
|2=|(
)|2+|(
)|2-2|(
)||(
)|cos60°=700.
故|
|=
km=10
km.
(2)设甲、乙两车t小时后的位置分别为P、Q,
则|
|=60t,|
|=60t.
当0≤t≤
时,|
|2=(30-60t)2+(10+60t)2-2(30-60t)(10+60t)cos60°;
当t>
时,|
|2=(60t-30)2+(10+60t)2-2(60t-30)(10+60t)cos120°.
上面两式可统一为|
|2=10800t2-3600t+700,
即|
|=10
km.
(3)因为|
|=10
,
故当t=
,即在第10分钟末时,两车距离最短,最短距离为20km.

则|
| AB |
| OA |
| OB |
| OA |
| OB |
故|
| AB |
| 700 |
| 7 |
(2)设甲、乙两车t小时后的位置分别为P、Q,
则|
| AP |
| BQ |
当0≤t≤
| 1 |
| 2 |
| PQ |
当t>
| 1 |
| 2 |
| PQ |
上面两式可统一为|
| PQ |
即|
| PQ |
| 108t2-36t+7 |
(3)因为|
| PQ |
| 108t2-36t+7 |
故当t=
| 1 |
| 6 |
点评:本题考查了向量在物理中的应用及余弦定理,通过设点将物理问题转化为数学问题,灵活的考查了学生分析问题解问题的能了,是个中档题.

练习册系列答案
相关题目
 如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.
如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.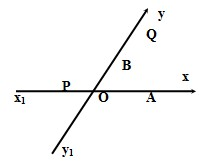 如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?
如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?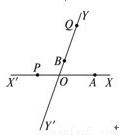
 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 km,乙离
km,乙离 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向步行.
的方向步行. 的式子表示
的式子表示