题目内容
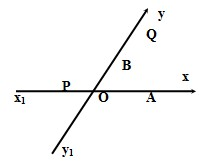 如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?
如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?分析:(1)连接AB,在三角形OAB中,由OA,OB及cos∠AOB的值,利用余弦定理即可求出AB的长;
(2)设运动的时间是t小时,两点运动的路程为4tkm,表示出此时的OA和OB,再由cos∠AOB的值,利用余弦定理表示出AB的长,根据t的范围,利用二次函数的性质即可求出两人距离最短时的时间t的值.
(2)设运动的时间是t小时,两点运动的路程为4tkm,表示出此时的OA和OB,再由cos∠AOB的值,利用余弦定理表示出AB的长,根据t的范围,利用二次函数的性质即可求出两人距离最短时的时间t的值.
解答:
解:(1)连接AB,在△OAB中,OA=3km,OB=1km,∠AOB=60°,
根据余弦定理得:AB2=OA2+OB2-2OA•OB•cos∠AOB=9+1-3=7,
解得:AB=
(km);
(2)A在O的右边,则t小时走的路为4t,OA=3-4t,OB=1+4t,
根据余弦定理得:AB=
,且0≤t<
,
设m=48t2-24t+7,可得m在[0,
)的最小值为m(
)=4,
则当t=
h时,两人的距离最短,最短距离为2.

解:(1)连接AB,在△OAB中,OA=3km,OB=1km,∠AOB=60°,
根据余弦定理得:AB2=OA2+OB2-2OA•OB•cos∠AOB=9+1-3=7,
解得:AB=
| 7 |
(2)A在O的右边,则t小时走的路为4t,OA=3-4t,OB=1+4t,
根据余弦定理得:AB=
| 48t2-24t+7 |
| 3 |
| 4 |
设m=48t2-24t+7,可得m在[0,
| 3 |
| 4 |
| 1 |
| 4 |
则当t=
| 1 |
| 4 |
点评:此题考查了余弦定理,特殊角的三角函数值以及二次函数的性质,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
 如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.
如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行. 如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.
如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.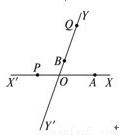
 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 km,乙离
km,乙离 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向步行.
的方向步行. 的式子表示
的式子表示