题目内容
【题目】【选修4-4：坐标系与参数方程】
在直角坐标系
中，曲线
的参数方程为
（
为参数），以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（Ⅰ）求曲线
的极坐标方程和
的直角坐标方程；
（Ⅱ）直线
与曲线
分别交于第一象限内的
，
两点，求
.
【答案】（1）
（2）
【解析】试题分析：（1）第（1）问，先把曲线
的参数方程化为直角坐标方程，再将直角坐标方程化为极坐标方程. 直接利用极坐标直角坐标互化公式将曲线
的极坐标方程化成直角坐标方程.（2）第（2）问，联立方程组求出A、B的极径，再求出|AB|.
试题解析：
（1）曲线
，
把
， 
，代入
，
得
，
化简得，曲线
的极坐标方程为
曲线
的极坐标方程为
所以曲线
的普通方程为
.
（2）依题意可设
所以
，
即
，所以
，
因为点
在一象限，所以
，即
，
所以
.
练习册系列答案
相关题目
【题目】20名高二学生某次数学考试成绩（单位：分）的频率分布直方图如图：
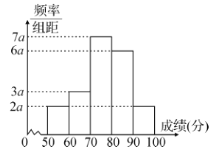
（1）求频率分布直方图中
的值；
（2）分别求出成绩落在
与
中的学生人数；
（3）从成绩在
的学生中任选2人，求此2人的成绩都在中的概率．
【题目】某单位有2000名职工，老年、中年、青年分布在管理、技术开发、营销、生产各部门中，如下表所示：
人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
老年 | 40 | 40 | 40 | 80 | 200 |
中年 | 80 | 120 | 160 | 240 | 600 |
青年 | 40 | 160 | 280 | 720 | 1 200 |
小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况，则应怎样抽样？
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会，则应怎样抽选出席人？
