Question

【题目】已知椭圆：的两个焦点分别为和，短轴的两个端点分别为和，点在椭圆上，且满足，当变化时，给出下列三个命题：

①点的轨迹关于轴对称；②的最小值为2；

③存在使得椭圆上满足条件的点仅有两个，

其中，所有正确命题的序号是__________．

Answer 1

【答案】①②

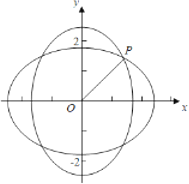
【解析】分析：运用椭圆的定义可得也在椭圆上，分别画出两个椭圆的图形，即可判断①正确；由图象可得当的横坐标和纵坐标的绝对值相等时，的值取得最小，即可判断②正确；通过的变化，可得③不正确.

详解：

椭圆的两个焦点分别为

和，

短轴的两个端点分别为和，

设，点在椭圆上，

且满足，

由椭圆定义可得，，

即有在椭圆上，

对于①，将换为方程不变，

则点的轨迹关于轴对称，故①正确.；

对于②，由图象可得，当满足，

即有，

即时，取得最小值，

可得时，

即有取得最小值为，故②正确；

对于③，由图象可得轨迹关于轴对称，且，

则椭圆上满足条件的点有个，

不存在使得椭圆上满足条件的点有个，故③不正确.

，故答案为①②.