题目内容
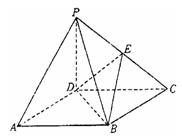
(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD 底面ABCD,PD=DC,E是PC的中点,作EF
底面ABCD,PD=DC,E是PC的中点,作EF PB交PB于点F
PB交PB于点F
(1)、证明:PA∥平面DEB;
(2)、证明:PB 平面EFD;
平面EFD;
(3)、设PD=1,求DF的长。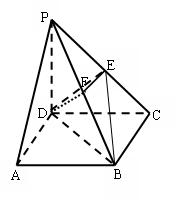
 底面ABCD,PD=DC,E是PC的中点,作EF
底面ABCD,PD=DC,E是PC的中点,作EF PB交PB于点F
PB交PB于点F(1)、证明:PA∥平面DEB;
(2)、证明:PB
 平面EFD;
平面EFD;(3)、设PD=1,求DF的长。

(1)证明略
(2)证明略
(3)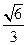
(2)证明略
(3)
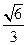
(1)连结AC交BD于O,由正方形ABCD得,O是AC的中点,又E是PC中点,∴EO∥PA,又PA 平面DEB,OE
平面DEB,OE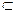 平面DEB,∴PA∥平面DEB。
平面DEB,∴PA∥平面DEB。
(2)侧棱PD 底面ABCD,∴ PD
底面ABCD,∴ PD BC,底面ABCD是正方形∴CD
BC,底面ABCD是正方形∴CD BC,又PD∩CD=D,
BC,又PD∩CD=D,
∴BC 平面PCD,DE
平面PCD,DE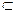 平面PCD,∴BC
平面PCD,∴BC DE,又由PD=DC,E是PC的中点得,DE
DE,又由PD=DC,E是PC的中点得,DE PC,而PC∩BC=C,∴DE
PC,而PC∩BC=C,∴DE 平面PCB,则DE
平面PCB,则DE PB,又EF
PB,又EF PB,DE∩EF=E,所以PB
PB,DE∩EF=E,所以PB 平面EFD。
平面EFD。
(3)由题意得DC=1,在正方形ABCD中,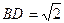 ,由侧棱PD
,由侧棱PD 底面ABCD得PD
底面ABCD得PD BD,由PB
BD,由PB 平面EFD得PB
平面EFD得PB 平面DF。则
平面DF。则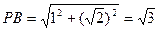 ,所以
,所以 ,
,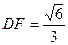 。
。
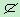 平面DEB,OE
平面DEB,OE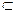 平面DEB,∴PA∥平面DEB。
平面DEB,∴PA∥平面DEB。(2)侧棱PD
 底面ABCD,∴ PD
底面ABCD,∴ PD BC,底面ABCD是正方形∴CD
BC,底面ABCD是正方形∴CD BC,又PD∩CD=D,
BC,又PD∩CD=D,∴BC
 平面PCD,DE
平面PCD,DE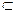 平面PCD,∴BC
平面PCD,∴BC DE,又由PD=DC,E是PC的中点得,DE
DE,又由PD=DC,E是PC的中点得,DE PC,而PC∩BC=C,∴DE
PC,而PC∩BC=C,∴DE 平面PCB,则DE
平面PCB,则DE PB,又EF
PB,又EF PB,DE∩EF=E,所以PB
PB,DE∩EF=E,所以PB 平面EFD。
平面EFD。(3)由题意得DC=1,在正方形ABCD中,
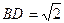 ,由侧棱PD
,由侧棱PD 底面ABCD得PD
底面ABCD得PD BD,由PB
BD,由PB 平面EFD得PB
平面EFD得PB 平面DF。则
平面DF。则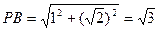 ,所以
,所以 ,
,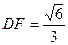 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
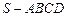 中,
中,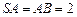 ,
,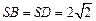 ,底面
,底面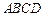 是菱形,且
是菱形,且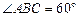 ,
,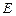 为
为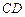 的中点.
的中点.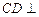 平面
平面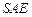 ;
;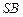 上是否存在点
上是否存在点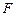 ,使得
,使得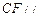 平面
平面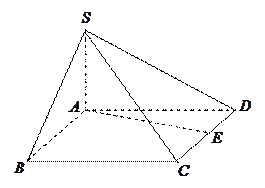
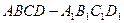 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,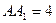 .
.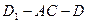 的平面角,并求出它的正切值;
的平面角,并求出它的正切值;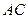 与
与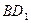 所成的角.
所成的角.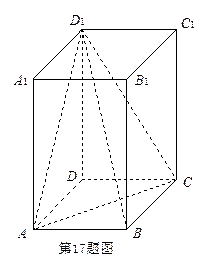
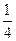 ,并求此时二面角A—PC—B的余弦值。
,并求此时二面角A—PC—B的余弦值。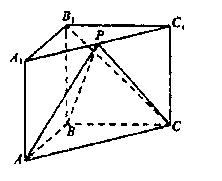
 0°。
0°。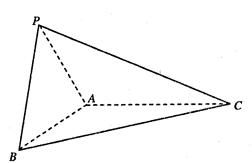
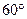 圈上有A、B两点,它们的经度相差
圈上有A、B两点,它们的经度相差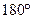 ,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )
,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )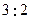 B.
B. 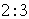 C.
C. 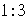 D.
D. 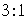
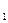 B
B