题目内容
(本小题满分13分)
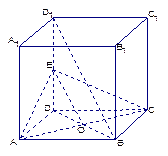
如图,三棱锥P—ABC中,平面PAC⊥平面BAC,AP=AB=AC=2,∠BAC=∠PAC=12 0°。
0°。
(I)求棱PB的长;
(II)求二面角P—AB—C的大小。
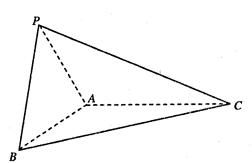
如图,三棱锥P—ABC中,平面PAC⊥平面BAC,AP=AB=AC=2,∠BAC=∠PAC=12
 0°。
0°。(I)求棱PB的长;
(II)求二面角P—AB—C的大小。

(I)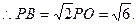
(II)二面角P—AB—C的大小为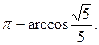
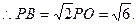
(II)二面角P—AB—C的大小为
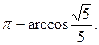
解:
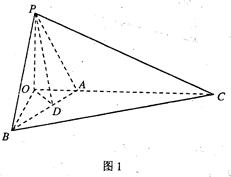
(I) 如图1,作PO⊥AC,垂足为O,连结OB,
如图1,作PO⊥AC,垂足为O,连结OB,
由已知得,△POC≌△BOC,则BO⊥AC。
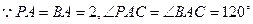 ,
,
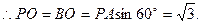 ………………3分
………………3分
∵平面PAC⊥平面BAC,∴PO⊥平面BAC,∴PO⊥OB,
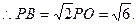 ………………6分
………………6分
(II)方
 法1:如图1,作OD⊥AB,垂足为D,连结PD,
法1:如图1,作OD⊥AB,垂足为D,连结PD, 由三垂线定理得,PD⊥AB。
由三垂线定理得,PD⊥AB。
则∠PDO为二面角P—AB—C的平面角的补角。 ………………8分
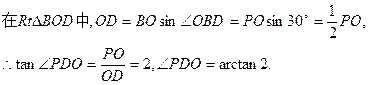
二面角P—AB— C的大小为
C的大小为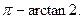 ………………12分
………………12分
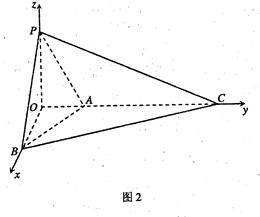
方法2:如图2 ,分别以OB,OC,OP为x轴,y轴,z轴,建立空间直角坐标系
,分别以OB,OC,OP为x轴,y轴,z轴,建立空间直角坐标系
O—xyz,则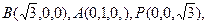
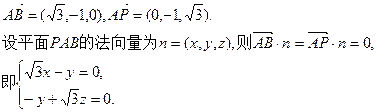
令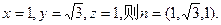 ………………9分
………………9分
又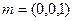 为面ABC的法向量。 ………………10分
为面ABC的法向量。 ………………10分
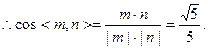
易知二面角P—AB—C的平面角为钝角,
故二面角P—AB—C的大小为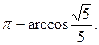 ………………12分
………………12分
(I)
 如图1,作PO⊥AC,垂足为O,连结OB,
如图1,作PO⊥AC,垂足为O,连结OB,由已知得,△POC≌△BOC,则BO⊥AC。
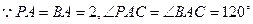 ,
,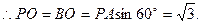 ………………3分
………………3分∵平面PAC⊥平面BAC,∴PO⊥平面BAC,∴PO⊥OB,
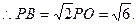 ………………6分
………………6分
(II)方

 法1:如图1,作OD⊥AB,垂足为D,连结PD,
法1:如图1,作OD⊥AB,垂足为D,连结PD, 由三垂线定理得,PD⊥AB。
由三垂线定理得,PD⊥AB。则∠PDO为二面角P—AB—C的平面角的补角。 ………………8分
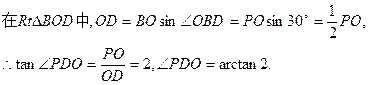
二面角P—AB—
 C的大小为
C的大小为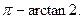 ………………12分
………………12分方法2:如图2
 ,分别以OB,OC,OP为x轴,y轴,z轴,建立空间直角坐标系
,分别以OB,OC,OP为x轴,y轴,z轴,建立空间直角坐标系O—xyz,则
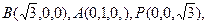
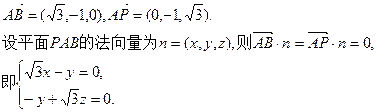
令
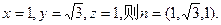 ………………9分
………………9分又
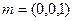 为面ABC的法向量。 ………………10分
为面ABC的法向量。 ………………10分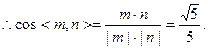
易知二面角P—AB—C的平面角为钝角,
故二面角P—AB—C的大小为
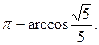 ………………12分
………………12分

练习册系列答案
相关题目
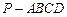 中,
中,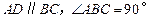 ,
,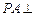 平面
平面 .PA=4,AD=2,AB=
.PA=4,AD=2,AB=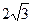 ,BC=6
,BC=6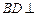 平面
平面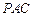 ;
;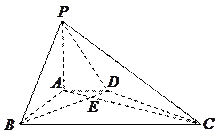
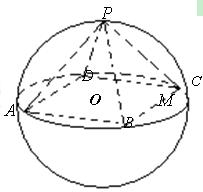
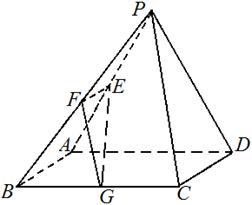
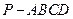 底面是正方形且四个顶点
底面是正方形且四个顶点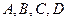 在球
在球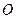 的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点
的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点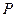 在球面
在球面 上且
上且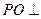 面
面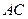 ,且已知
,且已知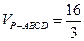 。
。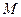 为
为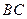 中点,求异面直线
中点,求异面直线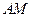 与
与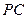 所成角的余弦值。
所成角的余弦值。
 底面ABCD,PD=DC,E是PC的中点,作EF
底面ABCD,PD=DC,E是PC的中点,作EF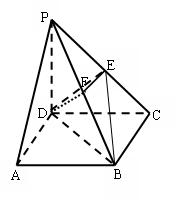
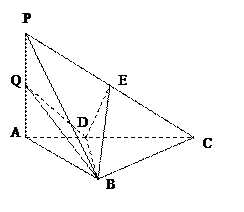
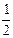 AB,N为AB
AB,N为AB 上一点,
上一点,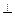 平面PAD;
平面PAD;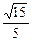 ?
?
 中,点
中,点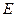 是
是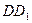 的中点.
的中点. 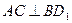 ;
;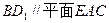 .
.