题目内容
19.已知x、y、z∈(0,+∞),且3x=4y=6z(1)求证:$\frac{1}{x}$+$\frac{1}{2y}$=$\frac{1}{z}$
(2)比较3x、4y、6z的大小.
分析 (1)设3x=4y=6z=t,化指数式为对数式后求出x,y,z,然后直接代入等式两端加以证明;
(2)因为x,y,z均为正数,利用作商法证明.
解答 解:(1)证明:设3x=4y=6z=t.∵x>0,y>0,z>0,∴t>1,lgt>0,
则x=log3t=$\frac{lgt}{lg3}$,y=log4t=$\frac{lgt}{lg4}$,z=log6t=$\frac{lgt}{lg6}$,
∴$\frac{1}{x}$+$\frac{1}{2y}$=$\frac{lg3}{lgt}$+$\frac{lg4}{2lgt}$=$\frac{lg3}{lgt}$+$\frac{lg2}{lgt}$=$\frac{lg6}{lgt}$=$\frac{1}{z}$
(2)∵3x>0,4y>0,且$\frac{3x}{4y}$=$\frac{3\frac{lgt}{lg3}}{4\frac{lgt}{lg4}}$=$\frac{3}{4}$•log34<1,
∴3x<4y,同理4y<6z,
故3x<4y<6z,
点评 本题考查了指数式和对数式的互化,考查了作商法进行正实数的大小比较,是基础题.

练习册系列答案
相关题目
9.若在区间[-1,2]中随机地取一个数x,则事件“0≤x≤2”发生的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.已知等比数列{an}的各项均为正数,且满足a3=a1+2a2,则$\frac{{a}_{9}+{a}_{10}}{{a}_{7}+{a}_{8}}$等于( )
| A. | 2+3$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 3-2$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
3.已知a>0,且a≠1,下列函数中,在其定义域内是单调函数而且又是奇函数的是( )
| A. | y=sinax | B. | y=logax2 | C. | y=ax-a-x | D. | y=tanax |
4.函数f(x)=$\frac{x}{(1-x)^{2}}$的单调递增区间是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-1,1) | D. | (-∞,1)∪(1,+∞) |
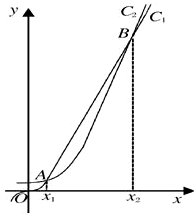 函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.
函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.