题目内容
1.在直角坐标系xoy中,设复数z满足|z-1|=1.(Ⅰ)求复数z所对应的点(x,y)的轨迹方程C;
(Ⅱ)以原点为极点,以x轴正半轴为极轴建立极坐标系,把(Ⅰ)中的曲线C化为极坐标方程,并判断其与曲线$ρcosθ+\sqrt{3}ρsinθ-3=0$的位置关系.
分析 (Ⅰ)首先根据复数的几何意义,把复数的模转化为圆的方程,进一步把圆的标准式转化为一般式,
(Ⅱ)根据题意把圆的一般式转化为极坐标方程.再把直线的极坐标式转化为普通式,再利用点到直线的距离公式判断直线和圆的关系.
解答 解:(Ⅰ)依题意复数z满足|z-1|=1.设复数z所对应的点为(x,y),
则点的轨迹方程C为:(x-1)2+y2=1.
(Ⅱ)首先把(x-1)2+y2=1转化为:x2+y2-2x=0,
再转化为极坐标方程为:ρ2-2ρcosθ=0,
∴ρ=2cosθ.
把$ρcosθ+\sqrt{3}ρsinθ-3=0化为直角坐标方程为x+\sqrt{3}y-3=0$.
$d=\frac{{|{1-3}|}}{{\sqrt{{1^2}+(\sqrt{3}}{)^2}}}=1$.
由于d=r
∴直线与圆相切.
点评 本题考查的知识要点:复数几何意义得应用,圆的普通式和标准式的转化,极坐标方程与普通方程的互化,点到直线的距离公式的应用,直线和圆的位置关系得应用,属于基础题型.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
11.已知在等差数列{an}中,a4=7,a6=13,则a8=( )
| A. | 18 | B. | 19 | C. | 17 | D. | 16 |
9.若函数f(x)=$\left\{\begin{array}{l}(2b-1)•{3^x}-b,x>0\\-{x^2}+(2-b)x,x≤0\end{array}$在R上为增函数,则实数b的取值范围为( )
| A. | $(\frac{1}{2},2]$ | B. | [1,2] | C. | (1,2] | D. | $(\frac{1}{2},2)$ |
6.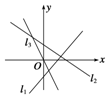 如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )
如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )
 如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )
如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )| A. | α1<α2<α3 | B. | α1<α3<α2 | C. | α3<α2<α1 | D. | α2<α1<α3 |
10.集合$M=\{x|x=kπ±\frac{π}{4},k∈Z\}$与$N=\{x|x=\frac{kπ}{2}+\frac{π}{4},k∈Z\}$之间的关系是( )
| A. | $M\begin{array}{l}?\\≠\end{array}N$ | B. | $N\begin{array}{l}?\\≠\end{array}M$ | C. | M=N | D. | M∩N=∅ |
11.已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的体积是( )


| A. | $8\sqrt{5}$ | B. | $\frac{{8\sqrt{5}}}{3}$ | C. | 6 | D. | 8 |