题目内容
过点P(2,4)引圆 的切线,其方程是_______________
的切线,其方程是_______________
x=2或3x-4y+10=0
【解析】
试题分析:由题意知,当直线斜率k存在时,设切线方程为y-4=k(x-2),即kx-y+4-2k=0
∴ ,解得
,解得 ,所以切线方程为3x-4y+10=0,
,所以切线方程为3x-4y+10=0,
当直线斜率不存在时,此时直线方程为x=2,经验证满足条件
综上,切线方程为x=2或3x-4y+10=0
考点:本题考查直线与圆的位置关系和点到直线的距离公式
点评:解决本题的关键是注意过点设直线时,考虑斜率存在和不存在两种情况

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
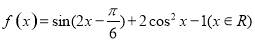
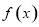 的单调递增区间;
的单调递增区间;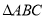 中,三内角
中,三内角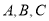 的对边分别为
的对边分别为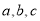 ,已知
,已知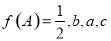 成等差数列,
成等差数列,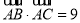 ,求
,求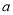 的值。
的值。 ,且
,且 是函数
是函数 的一个极值点.
的一个极值点. 的值;
的值; 的单调区间;
的单调区间; ,当函数
,当函数 在区间
在区间 上零点的个数为0个,3个时,实数
上零点的个数为0个,3个时,实数 的取值范围分别为多少?(参考数据:
的取值范围分别为多少?(参考数据: ,
, )
)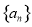 的前n项和为
的前n项和为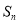 ,若
,若 ,
, ,则当
,则当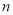 等于( )
等于( )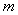 ,直线
,直线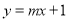 与圆
与圆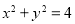 的位置关系一定是( )
的位置关系一定是( )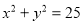
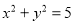
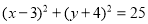
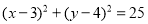
 为互相垂直的两个单位向量,则
为互相垂直的两个单位向量,则 ( )
( )
 C.
C. D.
D.
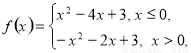 不等式
不等式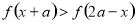 在
在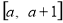 上恒成立,则实数
上恒成立,则实数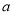 的取值范围是( )
的取值范围是( )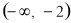 B.
B. 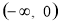 C.
C. 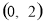 D.
D.