题目内容
(本题满分14分)已知函数 ,且
,且 是函数
是函数 的一个极值点.
的一个极值点.
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)设 ,当函数
,当函数 在区间
在区间 上零点的个数为0个,3个时,实数
上零点的个数为0个,3个时,实数 的取值范围分别为多少?(参考数据:
的取值范围分别为多少?(参考数据: ,
, )
)
(1)a=4;
(2)当 时,y=f(x)单调递增;当
时,y=f(x)单调递增;当 时,y=f(x)单调递减;当
时,y=f(x)单调递减;当 时,y=f(x)单调递减;
时,y=f(x)单调递减;
(3)0个时,m<2;3个时, ≤m<
≤m<
【解析】
试题分析:【解析】
(1) , 2分
, 2分
 得a=4. 3分
得a=4. 3分
(2)由(1)知 ,由
,由 ,解得
,解得 ,
,
由 及x>0得
及x>0得 或
或 ,
,
于是当 时,y=f(x)单调递增;
时,y=f(x)单调递增;
当 时,y=f(x)单调递减;
时,y=f(x)单调递减;
当 时,y=f(x)单调递减. 7分
时,y=f(x)单调递减. 7分
(3)令g(x)=f(x)-m=0,于是f(x)=m,所以函数y=g(x)在区间(0,5]上零点的个数是
y=f(x),x∈(0,5]与直线y=m交点的个数. 9分
由下表:
x | (0,1) | 1 | (1,3) | 3 | (3,5) | 5 |
| - | 0 | + | 0 | - | |
f(x) | ↘ | 极小值2 | ↗ | 极大值
| ↘ |
|
注意到: >
> >2,
>2,
所以函数f(x)在(0,5]的最小值为2,无最大值 11分
结合大致图象可知:
当m<2时,g(x)=f(x)-m的零点个数为0;
当m=2或m> 时,g(x)=f(x)-m的零点个数为1;
时,g(x)=f(x)-m的零点个数为1;
当2<m< 或m=
或m= 时,g(x)=f(x)-m的零点个数为2;
时,g(x)=f(x)-m的零点个数为2;
当 ≤m<
≤m< 时,g(x)=f(x)-m的零点个数为3. 14分
时,g(x)=f(x)-m的零点个数为3. 14分

考点:本题考查导数研究函数的单调性,极值;函数的零点的个数

练习册系列答案
相关题目

 ,则复数
,则复数  是虚数的充分必要条件是 ( )
是虚数的充分必要条件是 ( ) B.
B. C.
C. D.
D. 且
且 的前n项和为
的前n项和为 ,则下列结论一定成立的是( )
,则下列结论一定成立的是( ) ,则
,则 B.若
B.若 ,则
,则
 ,则
,则 >0 D.若
>0 D.若 ,则
,则 >0
>0
 的夹角为
的夹角为 ,且
,且 ,则
,则 与
与 的夹角为( )
的夹角为( ) B.
B. C.
C. D.
D.

 ,且
,且 ,求
,求 的值;
的值; 的最小正周期及单调递增区间.
的最小正周期及单调递增区间. 的公差为
的公差为 ,若
,若 成等比数列, 则
成等比数列, 则 ( )
( ) B.
B. C.
C. D.
D.
 的切线,其方程是_______________
的切线,其方程是_______________ 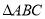 中,内角
中,内角 所对的边分别为
所对的边分别为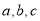 ,且
,且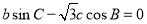 。
。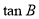 ;
; ,求
,求