��Ŀ����
15����ƽ��ֱ������ϵxOy�У���֪��$A��-\sqrt{2}��0��$��$B��\sqrt{2}��0��$��EΪ���㣬��ֱ��EA��ֱ��EB��б��֮��Ϊ�ˣ��ˡ�0����1����E�Ĺ켣���̣�������E�Ĺ켣�͵�A��B�ϲ���������C����������C����״��
��2������=-$\frac{1}{2}$ʱ��������C���ҽ���ΪF2������F2��ֱ��l1��l2�ֱ�����C�ڵ�P��Q�͵�M��N����P��M��Q��N����ʱ��˳�����У�����l1��l2�����ı���PMQN�������ֵ��
���� ��1���趯��E������Ϊ��x��y�����ɵ��$A��-\sqrt{2}��0��$��$B��\sqrt{2}��0��$��EΪ���㣬��ֱ��EA��ֱ��EB��б��֮��Ϊ�ˣ��ˡ�0����֪$\frac{y}{x+\sqrt{2}}$•$\frac{y}{x-\sqrt{2}}$=�ˣ��ˡ�0�����ɴ����������E�Ĺ켣C�ķ��̣�
��2����б�ʴ�������ڷֱ����ۣ�����ֱ������Բ����������Τ�ﶨ�����ҳ���ʽ��ȷ������ı���ʽ��������ý��ۣ�
��� �⣺��1���趯��E������Ϊ��x��y����
�ߵ�$A��-\sqrt{2}��0��$��$B��\sqrt{2}��0��$��EΪ���㣬��ֱ��EA��ֱ��EB��б��֮��Ϊ�ˣ��ˡ�0����
��$\frac{y}{x+\sqrt{2}}$•$\frac{y}{x-\sqrt{2}}$=�ˣ��ˡ�0����
��������x2-$\frac{{y}^{2}}{��}$=2��x�١�$\sqrt{2}$��
�ද��E�Ĺ켣C�ķ���Ϊ$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2��}$=1��
��=-1������C��ʾԲ���ˣ�-1��������y���ϵ���Բ��-1���ˣ�0��������x���ϵ���Բ���ˣ�0��������x���ϵ�˫���ߣ�
��2������=-$\frac{1}{2}$ʱ��������C��$\frac{{x}^{2}}{2}$+y2=1���ҽ���ΪF2��1��0��
��������l1��l2��һ��б�ʲ����ڣ���һ��б��Ϊ0����S=$\frac{1}{2}•2a•\frac{2{b}^{2}}{a}$=2����5�֣�
��������l1��l2��б�ʾ����ڣ���l1��y=k��x-1������Բ������������ȥy�ɵã�1+2k2��x2-4k2x+2k2-2=0��
��P��x1��y1����Q��x2��y2������x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$��x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$
��|PQ|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{2\sqrt{2}��1+{k}^{2}��}{1+2{k}^{2}}$
ͬ���ɵ�|MN|=$\frac{2\sqrt{2}��{k}^{2}+1��}{{k}^{2}+2}$����8�֣�
S=$\frac{1}{2}$|PQ||MN|=$\frac{4��{k}^{4}+2{k}^{2}+1��}{2{k}^{4}+5{k}^{2}+2}$=$\frac{4}{2+\frac{1}{{k}^{2}+\frac{1}{{k}^{2}}+2}}$
��${k}^{2}+\frac{1}{{k}^{2}}$��2����$\frac{16}{9}��S��2$����10�֣�
�ɣ�����������֪��Smin=$\frac{16}{9}$��Smax=2����12��
���� ���⿼�鶯��Ĺ켣���̵�������ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�������ã���ȷ��ʾ�ı���PMQN������ǹؼ���

 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{��}{2}$ | D�� | �� |
| A�� | f��2sin2����f��3sin3����f��4sin4�� | B�� | f��4sin4����f��3sin3����f��2sin2�� | ||
| C�� | f��3sin3����f��4sin4����f��2sin2�� | D�� | f��2sin2����f��4sin4����f��3sin3�� |
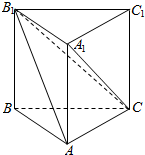 ��ͼ����ֱ������ABC-A1B1C1�У�AB��AC��AB=BB1=1��B1C=2��
��ͼ����ֱ������ABC-A1B1C1�У�AB��AC��AB=BB1=1��B1C=2��