题目内容
 四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=| 1 |
| 2 |
(1)求证:EF∥平面PAB;
(2)求二面角D-PA-B的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)取PB中点G,连结FG,AG,证明FG和AE平行且相等,AEFG为平行四边形,可得EF∥AG.再利用直线和平面平行的判定定理证得EF∥平面PAB.
(2)取PA的中点N,连接BN,DN,∠ANB=θ是二面角D-PA-B的平面角,即可得出结论.
(2)取PA的中点N,连接BN,DN,∠ANB=θ是二面角D-PA-B的平面角,即可得出结论.
解答:
(1)证明:取PB中点G,连结FG,AG,
 ∴FG平行且等于
∴FG平行且等于
BC,AE平行且等于
BC,
∴FG和AE平行且相等,
∴AEFG为平行四边形,
∴EF∥AG.
∵AG?平面PAB,而EF不在平面PAB内,
∴EF∥平面PAB.-------(6分)
(2)解:取PA的中点N,连接BN,DN---(8分)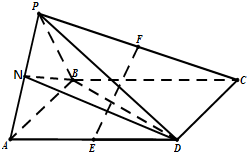
∵△PAB是等边三角形,∴BN⊥PA,
∵Rt△PBD≌Rt△ABD,∴PD=AD,∴AN⊥PB,
设∠ANB=θ是二面角D-PA-B的平面角--(10分)
∴BD⊥面PAB,BD⊥BN,
在Rt△DBN中,BD=
AB=2BN,-------------(12分)
tanθ=
=2,cosθ=
,
∴二面角D-PA-B的余弦值为:
---------(14分)
 ∴FG平行且等于
∴FG平行且等于| 1 |
| 2 |
| 1 |
| 2 |
∴FG和AE平行且相等,
∴AEFG为平行四边形,
∴EF∥AG.
∵AG?平面PAB,而EF不在平面PAB内,
∴EF∥平面PAB.-------(6分)
(2)解:取PA的中点N,连接BN,DN---(8分)

∵△PAB是等边三角形,∴BN⊥PA,
∵Rt△PBD≌Rt△ABD,∴PD=AD,∴AN⊥PB,
设∠ANB=θ是二面角D-PA-B的平面角--(10分)
∴BD⊥面PAB,BD⊥BN,
在Rt△DBN中,BD=
| 3 |
tanθ=
| BD |
| BN |
| ||
| 5 |
∴二面角D-PA-B的余弦值为:
| ||
| 5 |
点评:本题主要考查直线和平面平行的判定定理的应用,直线和平面垂直的判定定理的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( )
| A、130 | B、140 |
| C、150 | D、160 |
已知正四面体A-BCD的棱长为a,且a∈{x|x2-6x+5≤0},则
•(
+
)≥4的概率为( )
| AB |
| AC |
| AD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|