题目内容
已知倾斜角为60°的直线l通过抛物线x2=4y的焦点F,且与抛物线相交于A、B两点,则弦AB的长为
- A.4
- B.6
- C.10
- D.16
D
分析:设直线l的倾斜解为α,则l与y轴的夹角θ=90°-α,cotθ=tanα= ,sinθ=
,sinθ= ,由此能求出|AB|.
,由此能求出|AB|.
解答:设直线l的倾斜解为α,则l与y轴的夹角θ=90°-α,
cotθ=tanα= ,
,
sinθ= ,
,
|AB|=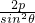 =
= .
.
故选D.
点评:本题考查抛物线的焦点弦的求法,解题时要注意公式|AB|=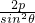 的灵活运用.
的灵活运用.
分析:设直线l的倾斜解为α,则l与y轴的夹角θ=90°-α,cotθ=tanα=
 ,sinθ=
,sinθ= ,由此能求出|AB|.
,由此能求出|AB|.解答:设直线l的倾斜解为α,则l与y轴的夹角θ=90°-α,
cotθ=tanα=
 ,
,sinθ=
 ,
,|AB|=
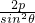 =
= .
.故选D.
点评:本题考查抛物线的焦点弦的求法,解题时要注意公式|AB|=
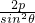 的灵活运用.
的灵活运用. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知倾斜角为60°的直线l通过抛物线x2=4y的焦点F,且与抛物线相交于A、B两点,则弦AB的长为( )
| A、4 | B、6 | C、10 | D、16 |
已知倾斜角为60°的直线 l过圆C:x2+2x+y2=0的圆心,则此直线l的方程是( )
A、
| ||||
B、x-
| ||||
C、x+
| ||||
D、
|