题目内容
19.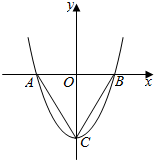 如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).
如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为$\frac{3\sqrt{3}}{2}$,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C,点O′,B′均落在此抛物线上,求此时O′的坐标.
分析 (1)通过求函数解析式,求出相应线段的长度,得到∠ABC的正切值,进而求出∠ABC度数;
(2)求出直线AC的方程和线段AC的长度,根据面积得出D到直线AC的距离,列方程组解出D的坐标;
(3)利用抛物线解析式设出O′,通过旋转60°,求出点B′的坐标,将点B′代入抛物线解析式即可求出.
解答 解:(1)把C(0,-3)代入f(x)得c=-3,∴f(x)=x2-3.
令f(x)=0得x2-3=0,解得x=±$\sqrt{3}$,∴A(-$\sqrt{3}$,0),B($\sqrt{3}$,0).
∴tan∠ABC=$\frac{OC}{OB}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,∴∠ABC=60°.
(2)由抛物线的对称性可知AC=BC,∴△ABC是等边三角形,∴AC=BC=2$\sqrt{3}$.
∵△ADC的面积为$\frac{3\sqrt{3}}{2}$,∴点D到AC的距离为$\frac{3}{2}$.
直线AC的方程为y=-$\sqrt{3}$x-3,即$\sqrt{3}$x+y+3=0.
设D(x,y),则$\left\{\begin{array}{l}{y={x}^{2}-3}\\{\frac{|\sqrt{3}x+y+3|}{2}=\frac{3}{2}}\\{x>0}\\{y<0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{\sqrt{15}-\sqrt{3}}{2}}\\{y=\frac{3-3\sqrt{5}}{2}}\end{array}\right.$.∴D点坐标为D($\frac{\sqrt{15}-\sqrt{3}}{2}$,$\frac{3-3\sqrt{5}}{2}$).
(3)设点O′(m,m2-3),∵O′,B′分别是由O,B($\sqrt{3}$,0)顺时针旋转60°得到的,
∴B′(m+$\frac{\sqrt{3}}{2}$,m2-$\frac{9}{2}$),∴m2-$\frac{9}{2}$=(m+$\frac{\sqrt{3}}{2}$)2-3,解得m=-$\frac{3\sqrt{3}}{4}$.
∴O′坐标为(-$\frac{3\sqrt{3}}{4}$,-$\frac{21}{16}$).
点评 本题考查了待定系数法求二次函数解析式,直线与圆锥曲线的关系,旋转变换,属于中档题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | x=3,y=10 | B. | x=6,y=10 | C. | x=3,y=15 | D. | x=6,y=15 |
| A. | $g(x)=\sqrt{x}$ | B. | $g(x)=\sqrt{x+4}$ | C. | g(x)=x2+1 | D. | g(x)=x2+4 |
| A. | y=-$\frac{1}{x}$ | B. | y=ln(x+5) | C. | y=x2-1 | D. | y=x|x| |
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{3}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
| 单价x(元) | 4.4 | 4.1 | 3.6 | 3.2 | 2.7 | 1.8 |
| 销量y(千件) | 1.6 | 2 | m | 4.8 | 5.2 | 6 |
| A. | 4.2 | B. | 4.4 | C. | 4.6 | D. | 4.7 |