题目内容
9.(x+1)(x-3)5的展开式中含x3项的系数为-180.分析 把(x-3)5的按照二项式定理展开,可得(x+1)(x-3)5的展开式中含x3项的系数.
解答 解:∵(x+1)(x-3)5=(x+1)(${C}_{5}^{0}$•x5+${C}_{5}^{1}$•x4•(-3)+${C}_{5}^{2}$•x3•(-3)2+${C}_{5}^{3}$•x2•(-3)3+${C}_{5}^{4}$•x(-3)4+${C}_{5}^{5}$•(-3)5),
故 展开式中含x3项的系数为${C}_{5}^{3}$•(-3)3+${C}_{5}^{2}$•(-3)2=-180,
故答案为:-180.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
20.现有1角、2角、5角、1元、2元、5元、10元、50元人民币各一张,100元人民币2张,从中至少取一张,共可组成不同的币值种数( )
| A. | 1024种 | B. | 1023种 | C. | 767种 | D. | 1535种 |
17.若a?α,b?β,a∩b=M,则( )
| A. | M∉β | B. | M?β | C. | M?α | D. | M∈β |
14.若$\underset{lim}{n→∞}$$\frac{f({x}_{0})-f({x}_{0}+△x)}{△x}$=1,则f′(x0)等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | -1 |
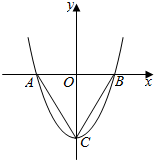 如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).
如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).