题目内容
11.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格试销,得到如下数据:| 单价x(元) | 4.4 | 4.1 | 3.6 | 3.2 | 2.7 | 1.8 |
| 销量y(千件) | 1.6 | 2 | m | 4.8 | 5.2 | 6 |
| A. | 4.2 | B. | 4.4 | C. | 4.6 | D. | 4.7 |
分析 计算样本中心点,根据线性回归方程恒过样本中心点,列出方程,求解即可得到结论.
解答 解:由题意,$\overline{x}$=3.96,$\overline{y}$=3.72+0.2m,
∵y关于x的线性回归方程为$\widehat{y}$=-2x+10.6,
根据线性回归方程必过样本的中心,
∴3.72+0.2m=-2×3.96+10.6,
∴m=4.4.
故选:B.
点评 本题考查线性回归方程的运用,解题的关键是利用线性回归方程恒过样本中心点,这是线性回归方程中最常考的知识点.属于基础题.

练习册系列答案
相关题目
1.已知函数f(x)=sin2(ωx)-$\frac{1}{2}$(ω>0)的最小正周期为$\frac{π}{2}$,若将其图象沿x轴向右平移a个单位(a>0),所得图象关于原点对称,则实数a的最小值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
6.在△ABC中,内角A,B,C的对边分别为a,b,c,若$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{4}{3}$,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
3.已知抛物线y2=4x+a的焦点在圆(x-1)2+(y+1)2=5的内部,则a的取值范围区间( )
| A. | (-4,12) | B. | (-1,3) | C. | (-2,2) | D. | (-8,8) |
20.现有1角、2角、5角、1元、2元、5元、10元、50元人民币各一张,100元人民币2张,从中至少取一张,共可组成不同的币值种数( )
| A. | 1024种 | B. | 1023种 | C. | 767种 | D. | 1535种 |
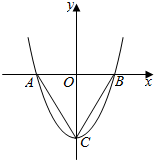 如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).
如图.在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A、B,(点A在点B的左侧),与y轴交点C(0,-3).