题目内容

4．若函数y=ax+b的部分图象如图所示，则（　　）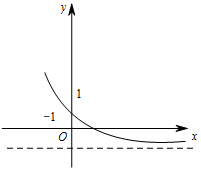
A．0＜a＜1，-1＜b＜0B．0＜a＜1，0＜b＜1C．1＜a，-1＜b＜0D．1＜a，0＜b＜1

分析 函数y=ax+b的图象由函数y=ax的图象向上平移b个单位得到，结合指数函数的图象和性质，函数图象的平移变换法则，可得答案．

解答 解：∵函数y=ax+b的图象由函数y=ax的图象向上平移b个单位得到，
由函数y=ax+b为减函数，可得0＜a＜1，
由函数y=ax+b的图象与y轴交点在原点与（0，1）点之间，
故-1＜b＜0，
故选：A

点评 本题考查的知识点是函数的图象，指数函数的图象和性质，函数图象的平移变换法则，难度中档．

练习册系列答案
相关题目
14．过点M（1，1）作斜率为$-\frac{1}{2}$的直线与椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$相交于A，B，则直线AB的方程x+2y-3=0；若M是线段AB的中点，则椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$．
15．已知等比数列{an}的前n项和为Sn，若S3=12，S6=60，则S9=（　　）
A．192B．300C．252D．360
12．为了得到函数y=2×2x的图象，可以把函数y=2x的图象（　　）
A．向左平移1个单位长度B．向右平移1个单位长度
C．向左平移2个单位长度D．向右平移2个单位长度
19．幂函数f（x）=kxα（k，α∈R）的图象经过点$（{\frac{1}{3}\;，\;\;9}）$，则k+α=-1．
9．函数f（x）的定义域为D，若存在闭区间[m，n]⊆D，使得函数f（x）满足以下两个条件：
（1）f（x）在[m，n]上是单调函数；
（2）f（x）在[m，n]上的值域为[2m，2n]，则称区间[m，n]为y=f（x）的“倍值区间”．下列函数中存在“倍值区间”的有①③④（填上所有正确的序号）
①f（x）=x2（x≥0）
②f（x）=ex（x∈R）
③$f（x）=\frac{4x}{{{x^2}+1}}（{x≥0}）$
④$f（x）={log_2}（{{2^x}-\frac{1}{8}}）$．
16．函数f（x）=2cos（$\frac{x}{2}+\frac{π}{4}$）（x∈R）的最小正周期为（　　）
A．$\frac{π}{2}$B．πC．2πD．4π
13．已知函数f（x）=$\left\{\begin{array}{l}{-（x+1）^{2}+1，x＜0}\\{{2}^{x}-1，x≥0}\end{array}\right.$，若函数g（x）=f（x）-a有三个零点，则实数a的取值范围是（　　）
A．（0，1）B．[0，1）C．（0，1]D．[0，1]
14．已知集合M={1，2，3}，N={1，3，4}，则M∩N=（　　）
A．{1，3}B．{1，2，3，4}C．{2，4}D．{1，3，4}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网