题目内容
17.(2x+1)(2-x)6的展开式中,x6的系数为-23(数字作答).分析 在(2-x)6二项展开式的通项公式中,令x的幂指数等于5,6,即可求得展开式中x6的系数.
解答 解:(2-x)6的展开式的通项公式为 Tr+1=C6r•(-1)r•26-r•xr,
可得(2x+1)(2-x)6的展开式中,x6的系数为2C65•(-1)5•21+C66•(-1)6•26-6=-23.
故答案为:-23.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
8.记a=sin(cos2016°),b=sin(sin2016°),c=cos(sin2016°),d=cos(cos2016°),则( )
| A. | d>c>b>a | B. | d>c>a>b | C. | c>d>b>a | D. | a>b>d>c |
5.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}(x∈[0,+∞))}\\{{a}^{x}+{a}^{2}-3a+1(x∈(-∞,0))}\end{array}\right.$在区间(-∞,+∞)是增函数,则常数a的取值范围是( )
| A. | 1≤a≤2 | B. | a<1或a≥2 | C. | 1<a≤2 | D. | a<1或a>2 |
6.已知A,B两地间的距离为20km,B,C两地间的距离为40km,现测得∠ABC=120°,则A,C两地间的距离为( )
| A. | 20km | B. | 20$\sqrt{3}$km | C. | 20$\sqrt{5}$km | D. | 20$\sqrt{7}$km |
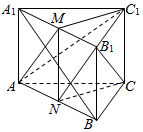 如图,正三棱柱ABC-A1B1C1的底面边长为2,AC1⊥A1B,M是A1B1的中点,N是AB中点,求证:
如图,正三棱柱ABC-A1B1C1的底面边长为2,AC1⊥A1B,M是A1B1的中点,N是AB中点,求证: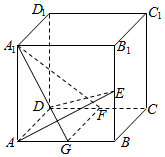 如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.
如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.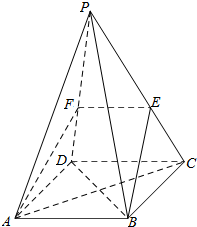 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.