题目内容

8．一个球的表面积为36π，则这个球体的体积为（　　）
A．18πB．36πC．72πD．108π

分析 利用球的表面积，我们可以求得球的半径，利用体积公式就可以求出球的体积．

解答 解：设球的半径为R，则
∵球的表面积为36π，
∴4πR2=36π
∴R=3cm
∴球的体积V=$\frac{4}{3}$πR3=$\frac{4}{3}$π×27=36π．
故选：B．

点评 本题主要考查球的表面积与体积公式，正确运用公式是解题的关键．

练习册系列答案
相关题目
8．已知f（x）=lg（2x+2-x），下列命题：①定义域为R；②值域为R；③在定义域上为偶函数；④在（-∞，0）上为减函数；⑤函数g（x）=f（x）-2恰有两个零点．其中正确命题是①③④⑤．（只要填写正确命题的序号）
9．函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x\\;x≥1}\\{{2}^{x}\\;x＜1}\end{array}\right.$的值域为（　　）
A．（-∞，0]B．（-∞，2）C．[0，+∞）D．（2，+∞）
16．直线l是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右准线，以原点O为圆心且过双曲线焦点的圆被直线l分成弧长为2：1的两段，则双曲线的离心率为（　　）
A．$\sqrt{5}$B．$\sqrt{3}$C．$\frac{{\sqrt{2}}}{2}$D．$\sqrt{2}$
3．已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1（a＞0，b＞0）的离心率为$\sqrt{2}$，且双曲线与抛物线x2=-4$\sqrt{3}$y的准线交于A，B，S△OAB=$\sqrt{3}$，则双曲线的实轴长2$\sqrt{2}$．
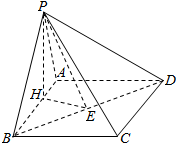13．如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=3，AD=2，PA=2，PD=2$\sqrt{2}$，∠PAB=60°．
（1）证明AD⊥平面PAB；
（2）求异面直线PC与AD所成的角的正切值；
（3）求二面角P-BD-A的正切值．
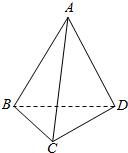20．如图，在四面体ABCD中，已知∠ABD=∠CBD=60°，AB=BC=2，
（Ⅰ） 求证：AC⊥BD；
（Ⅱ）若平面ABD⊥平面CBD，且BD=$\frac{5}{2}$，求二面角C-AD-B的余弦值．
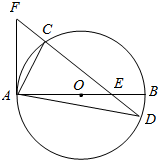17．如图AB是圆O的直径，AF⊥AB，弦CD交AB、AF分别于E、F，交圆于点C．
（1）证明：AF•DA=AC•DF
（2）若圆的半径为2，OE=EB=$\frac{1}{2}$AF，ED=$\frac{3}{2}$，求CF的长．
18．已知球面上有A、B、C三点，BC=2$\sqrt{3}$，AB=AC=2，若球的表面积为20π，则球心到平面ABC的距离为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网