题目内容
9.函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x\\;x≥1}\\{{2}^{x}\\;x<1}\end{array}\right.$的值域为( )| A. | (-∞,0] | B. | (-∞,2) | C. | [0,+∞) | D. | (2,+∞) |
分析 对x分类讨论,分别利用对数函数与指数函数的单调性即可得出.
解答 解:当x≥1时,f(x)≤$lo{g}_{\frac{1}{2}}1$=0;
当x<1时,0<f(x)<21=2.
综上可得:函数f(x)的值域为:(-∞,2).
故选:B.
点评 本题考查了对数函数与指数函数的单调性、分段函数的值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.设F1,F2分别是椭圆x2+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<1)的左,右焦点,过F1的直线L与椭圆相交于A,B两点,|AB|=$\frac{4}{3}$,直线L的斜率为1,则b的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
8.一个球的表面积为36π,则这个球体的体积为( )
| A. | 18π | B. | 36π | C. | 72π | D. | 108π |
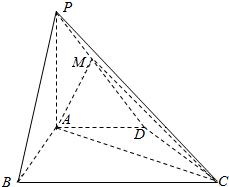 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点. 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.