题目内容
7．定义域为R的函数f（x）为奇函数，若f（x+2）为偶函数，且f（1）=1，则f（8）+f（17）=（ ）| A． | -2 | B． | -1 | C． | 0 | D． | 1 |
分析 根据函数奇偶性的性质进行转化求解即可．
解答 解：∵f（x+2）为偶函数，
∴f（-x+2）=f（x+2），
∵f（x）是奇函数，
∴f（-x+2）=-f（x-2），
即f（x+2）=-f（x-2），
即f（x+4）=-f（x），
则f（x+8）=-f（x+4）=f（x），
则f（9）=f（1）=1，
f（8）=f（0），
∵f（x）是奇函数，
∴f（0）=0，
即f（8）=f（0）=0，
则f（8）+f（9）=1+0=1．
故选：D．
点评 本题主要考查函数值的计算，根据函数奇偶性的性质求出函数的周期性是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．已知四棱锥P-ABCD的底面ABCD是矩形，PA⊥底面ABCD，点E、F是棱PC、PD的中点，则：①AB⊥PD；②平面PBC与平面ABCD垂直；③△PCD的面积大于△PAB的面积；④直线AE与直线BF是异面直线．其中正确结论的序号是（ ）
| A． | ①② | B． | ①④ | C． | ②④ | D． | ①③ |
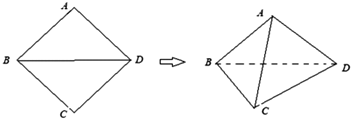
15．已知一个四面体其中五条棱的长分别为1，1，1，1，$\sqrt{2}$，则此四面体体积的最大值是（ ）
| A． | $\frac{{\sqrt{3}}}{12}$ | B． | $\frac{{\sqrt{2}}}{12}$ | C． | $\frac{{\sqrt{2}}}{4}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
19．若a是实数，则“a2≠9”是“a≠3”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
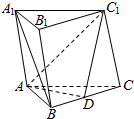如图，正三棱柱ABC-A1B1C1的各棱均相等，AB=2，D是BC上的一点，AD⊥C1D．