题目内容
15.已知一个四面体其中五条棱的长分别为1,1,1,1,$\sqrt{2}$,则此四面体体积的最大值是( )| A. | $\frac{{\sqrt{3}}}{12}$ | B. | $\frac{{\sqrt{2}}}{12}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 由题意,四面体的一个面为直角三角形,一个侧面为等边三角形,这两个面互相垂直时,四面体体积最大.即可求出四面体体积的最大值.
解答 解:由题意,四面体的一个面为直角三角形,一个侧面为等边三角形,这两个面互相垂直时,四面体体积最大.
四面体体积的最大值是$\frac{1}{3}×\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{12}$.
故选:A.
点评 本题考查的知识点是棱锥的体积公式及其几何特征,其中根据棱锥的几何特征,分析出四面体的一个面为直角三角形,一个侧面为等边三角形,这两个面互相垂直时,四面体体积最大是解答问题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
3.使|x-4|+|x-3|<a有实数解a的取值范围是( )
| A. | a>7 | B. | 1<a<7 | C. | a>1 | D. | a<7 |
7.定义域为R的函数f(x)为奇函数,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(17)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
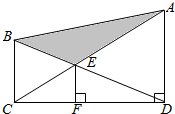 如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.
如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.