题目内容

2．已知A=$\{x∈Z|{log_2}x＜4\}，B=\{x|\frac{5}{3-x}≥1\}$，则A∩B的元素个数为（　　）
A．2B．3C．4D．5

分析 求出A中不等式的解集，找出解集中的整数解确定出A，求出B中不等式的解集确定出B，找出A与B的交集，即可做出判断．

解答 解：由A中不等式变形得：log2x＜4=log216，即0＜x＜16，x∈Z，
∴A={1，2，3，4，5，6，7，8，9，10，11，12，13，14，15}，
由B中不等式变形得：$\frac{5}{3-x}$-1≥0，
整理得：$\frac{2+x}{3-x}$≥0，即$\frac{x+2}{x-3}$≤0，
解得：-2≤x＜3，即B=[-2，3），
∴A∩B={1，2}，即A∩B的元素个数为2，
故选：A．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
12．已知a=log3$\frac{1}{4}$，b=3${\;}^{-\frac{1}{3}}$，c=log${\;}_{\frac{1}{2}}$2，则（　　）
A．a＜b＜cB．b＜c＜aC．a＜c＜bD．c＜a＜b
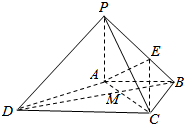13．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB∥DC，AB⊥BC，且PA=AB=BC=$\frac{1}{2}$CD，BE=$\frac{1}{3}$BP．
（1）求证：PD∥平面AEC；
（2）求二面角A-CE-P的余弦值．
10．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F，直线：x=$\frac{{a}^{2}}{c}$与两条渐近线交于P，Q两点，如果△PQF是等边三角形，则双曲线的离心率e的值为2．
17．如图1，在直角梯形ABCD中，AB∥CD，AB⊥AD，且AB=AD=$\frac{1}{2}$CD=1．现以AD为一边向形外作正方形ADEF，然后沿边AD将正方形AEFD翻折，使平面ADEF与平面ABCD垂直，M为ED的中点，如图2．
（1）求证：AM∥平面BEC；
（2）求证：BC⊥平面BDE；
（3）求点D到平面BEC的距离．
7．定义域为R的函数f（x）为奇函数，若f（x+2）为偶函数，且f（1）=1，则f（8）+f（17）=（　　）
A．-2B．-1C．0D．1
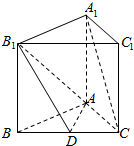14．已知正三棱柱ABC-A1B1C1中，BC=1，D是棱BC上的动点．
（1）当D在何处时，A1C∥平面AB1D，并证明之．
（2）若D为BC中点，且直线AB1与平面ABC成60°角，试求二面角B-AB1-D的余弦值大小．
11．如图，在Rt△ABC中，∠ACB=90°，∠B=30°，D，E分别为AB，CD的中点，AE的延长线交CB于F，现将△ACD沿CD折起，折成二面角A-CD-B，连接AF，M，N分别为AD，BC的中点．
（1）求证：MN∥面AEF；
（2）当∠AEF=120°时，求二面角A-BD-E大小的余弦值．
12．求下列极限．
（1）$\underset{lim}{x→0}$$\frac{sinsinx}{x}$
（2）$\underset{lim}{x→0}$$\frac{sin4x}{\sqrt{x+1}-1}$
（3）$\underset{lim}{x→0}$（$\frac{1+x}{1-x}$）${\;}^{\frac{1}{x}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网