Question

函数f(x)=|2x³-9x²+12x|,x∈［-,］的最大值为（    ）

A.0              B.4                C.              D.5

Answer 1

解析：函数f(x)在［-,］上连续，故它存在最大值与最小值.因为

f(x)=|2x³-9x²+12x|=|x(2x²-9x+12)|

=

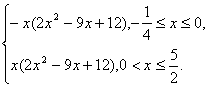
    所以f′(x)=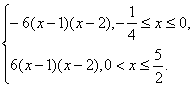

    函数f(x)在x=0处不可导，且由f′(x)=0.

    得x₁=1,x₂=2.可得f(0)=0,f(1)=5,f(2)=4.

    又区间两端点为-，可得f(-)=,f()=5.

    通过比较可知：函数f(x)=0在x=0处取最小值0，

    在x=1和x=处都取得最大值5.

答案：D