题目内容
20.定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)=$\frac{f(b)-f(a)}{b-a}$,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点,例如y=|x|是[-2,2]上的平均值函数,0就是它的均值点,若函数f(x)=x2-mx-1是[-1,1]上的“平均值函数”,则实数m的取值范围是( )| A. | [-1,1] | B. | (0,2) | C. | [-2,2] | D. | (0,1) |
分析 由已知得关于x的方程x2-mx-1=$\frac{f(1)-f(-1)}{1-(-1)}$在(-1,1)内有实数根.从而x2-mx+m-1=0,进而x=m-1为均值点,由此能求出实数m的取值范围.
解答 解:∵函数f(x)=-x2+mx-1是区间[-1,1]上的平均值函数,
∴关于x的方程x2-mx-1=$\frac{f(1)-f(-1)}{1-(-1)}$在(-1,1)内有实数根.
由x2-mx-1=$\frac{f(1)-f(-1)}{1-(-1)}$,得x2-mx+m-1=0,解得x=m-1,x=1.
又1∉(-1,1)
∴x=m-1必为均值点,即-1<m-1<1,∴0<m<2.
∴所求实数m的取值范围是0<m<2.
故选:B.
点评 本题考查实数取值范围的求法,是基础题,解题时要认真审题,注意“平均值函数”的性质的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
10.已知集合A={x∈N|x≤1},B={x|-1≤x≤2},则A∩B=( )
| A. | {0,1} | B. | {-1,0,1} | C. | [-1,1] | D. | {1} |
11.将函数f(x)=$\sqrt{3}$sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移$\frac{π}{6}$个单位,得到函数y=g(x)的图象,则y=g(x)的一条对称轴是( )
| A. | $x=-\frac{π}{6}$ | B. | $x=-\frac{π}{4}$ | C. | $x=\frac{π}{3}$ | D. | $x=\frac{π}{2}$ |
9.一个生物研究性学习小组,为了研究平均气温与一天内某豆类胚芽生长之间的关系,他们分别记录了4月6日至4月11日的平均气温x(℃)与该豆类胚芽一天生长的长度y(mm),得到如下数据:
该小组的研究方案是:先从这六组数据中选取6日和11日的两组数据作为检验数据,用剩下的4组数据即:7日至10日的四组数据求出线性回归方程.
(1)请按研究方案求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)用6日和11日的两组数据作为检验数据,并判断该小组所得线性回归方程是否理想.(若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm,则认为该方程是理想的)
参考公式:$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$.
| 日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
| 平均气温x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 一天生长的长度y(mm) | 22 | 25 | 29 | 26 | 16 | 12 |
(1)请按研究方案求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)用6日和11日的两组数据作为检验数据,并判断该小组所得线性回归方程是否理想.(若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm,则认为该方程是理想的)
参考公式:$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$.
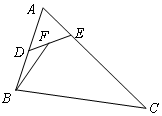 如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,
如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,