题目内容
下列四个判断:
①某校高三(1)班的人和高三(2)班的人数分别是m和n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为
;
②对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),由样本数据得到回归方程
=
x+
必过样本点的中心(
,
);
③调查某单位职工健康状况,其青年人数为300,中年人数为150,老年人数为100,现考虑采用分层抽样,抽取容量为22的样本,则青年中应抽取的个体数为12;
④对分类变量X与Y的随机变量K2的观测值k,k越小,“X与Y有关系”的把握程度越大.
其中正确的个数有( )
①某校高三(1)班的人和高三(2)班的人数分别是m和n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为
| a+b |
| 2 |
②对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),由样本数据得到回归方程
| ? |
| y |
| ? |
| b |
| ? |
| a |
. |
| x |
. |
| y |
③调查某单位职工健康状况,其青年人数为300,中年人数为150,老年人数为100,现考虑采用分层抽样,抽取容量为22的样本,则青年中应抽取的个体数为12;
④对分类变量X与Y的随机变量K2的观测值k,k越小,“X与Y有关系”的把握程度越大.
其中正确的个数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据加权平均数的公式知①不正确,
根据线性回归方程过样本中心点知②正确,
先求出每个个体被抽到的概率,用青年职工的总人数乘以此概率的值,即得应从青年职工中抽取的人数,
根据独立性检验的方法和步骤,可判断④.
根据线性回归方程过样本中心点知②正确,
先求出每个个体被抽到的概率,用青年职工的总人数乘以此概率的值,即得应从青年职工中抽取的人数,
根据独立性检验的方法和步骤,可判断④.
解答:
解:①当某校高三一班和高三二班的人数分别是m,n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为
,故①不正确;
②根据回归直线y=bx+a必过样本中心点,得到一定过点(
,
),故②正确;
③每个个体被抽到的概率等于
=
,则300×
=12,
则青年层中应抽取的个体数为 12,故③正确;
④对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越小,故④不正确;
则真命题为②③,
故选:C.
| am+bn |
| m+n |
②根据回归直线y=bx+a必过样本中心点,得到一定过点(
. |
| x |
. |
| y |
③每个个体被抽到的概率等于
| 22 |
| 300+150+100 |
| 1 |
| 25 |
| 1 |
| 25 |
则青年层中应抽取的个体数为 12,故③正确;
④对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越小,故④不正确;
则真命题为②③,
故选:C.
点评:本题考查命题真假的判断,包括回归分析,频率分布直方图,众数,平均数和中位数,本题解题的关键是正确进行有关数据的运算,本题是一个基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点为抛物线x2=4y的焦点,则直线l的方程为( )
| A、2x+3y-3=0 |
| B、x-y-1=0 |
| C、x+y-1=0 |
| D、x-y+1=0 |
在区间(0,1)内任取两个数,则这两个数之和小于
的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC中,若a=1,c=2,B=30°,则△ABC的面积为( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
若某空间几何体的三视图如图所示,则该几何体的体积是( )
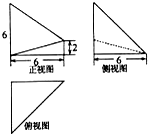

| A、16 | B、32 | C、48 | D、144 |
已知角α的终边过点P(
,-
),则sinα的值为( )
| 1 |
| 3 |
2
| ||
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|