题目内容
15.化简:(1)$\frac{cosα}{sin\frac{α}{2}cos\frac{α}{2}}$;
(2)$\frac{4si{n}^{2}α}{1-cos2α}$.
分析 (1)利用二倍角的正弦函数化简求解即可.
(2)利用二倍角的余弦函数化简求解即可.
解答 解:(1)$\frac{cosα}{sin\frac{α}{2}cos\frac{α}{2}}$=$\frac{2cosα}{sinα}$=2cotα;
(2)$\frac{4si{n}^{2}α}{1-cos2α}$=$\frac{4si{n}^{2}α}{1-(1-2si{n}^{2}α)}$=2.
点评 本题考查二倍角公式的应用,三角函数化简求值,考查计算能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3.假如你是一名交通部门工作人员,你打算向市长报告国家对本市26个公路项目的平均资金数额,其中一条新公路的建设投资为2000万元人民币,另外25个项目的投资是20~100万元,中位数是25万元,平均数是100万元,众数是20万元,你会选择哪一个数字特征来表示国家对每一个项目投资的平均金额?( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 标准差 |
7.若不等式组$\left\{\begin{array}{l}{x+ay+1≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$,表示的平面区域的面积等于4,则a=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
9.已知2a=3b=k(k≠1),且2a+b=2ab,则实数k的值为( )
| A. | 18 | B. | 18 或-18 | C. | $3\sqrt{2}$或 $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
 如图所示,秋千拉绳长3m,静止时踩板离地面高度为0.5m,某同学荡秋千时,踩板离地面最高处2m(左右对称),求该同学荡过的最大幅度AB.
如图所示,秋千拉绳长3m,静止时踩板离地面高度为0.5m,某同学荡秋千时,踩板离地面最高处2m(左右对称),求该同学荡过的最大幅度AB.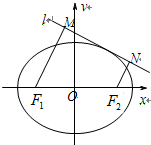 已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.
已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.