题目内容
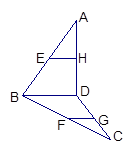
如图,在多面体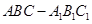 中,四边形
中,四边形 是正方形,
是正方形,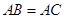 ,
, ,
,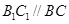 且
且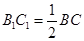 ,二面角
,二面角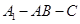 是直二面角
是直二面角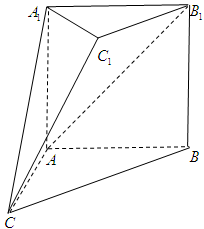
(1)求证: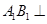 平面
平面 ;
;
(2)求证: 平面
平面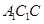 。
。
(1)因为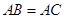 ,
, 所以
所以 ,四边形
,四边形 是正方形,所以
是正方形,所以 ,所以
,所以 平面
平面 ,
, ,所以
,所以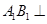 平面
平面 (2)取
(2)取 的中点
的中点 ,连接
,连接 因为
因为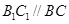 且
且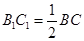 故
故 ,且
,且 又
又 且
且 ,所以
,所以 ,且
,且 所以
所以 是平行四边形,所以
是平行四边形,所以 ,
, 平面
平面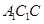 同理
同理 平面
平面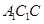 ,所以平面
,所以平面 平面
平面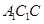 ,所以
,所以 平面
平面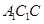
解析试题分析:(1)因为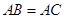 ,
,
所以 ,所以
,所以 。
。
又因为四边形 是正方形,所以
是正方形,所以 。
。
又因为 ,所以
,所以 平面
平面 。
。
易知
所以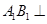 平面
平面
(2)取 的中点
的中点 ,连接
,连接

因为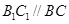 且
且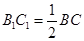
所以 是平行四边形,故
是平行四边形,故 ,且
,且
又 且
且 ,所以
,所以 ,且
,且
所以 是平行四边形
是平行四边形
所以 ,所以
,所以 平面
平面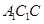
同理 平面
平面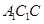
又因为 ,所以平面
,所以平面 平面
平面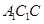
所以 平面
平面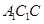
考点:线面垂直平行的判定
点评:判定直线与平面平行常利用平面外一直线与平面内一直线平行或两面平行实现;判定线面垂直常利用直线垂直于平面内两相交直线方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
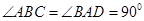 ,
,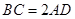 ,
,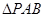 和
和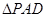 都是等边三角形.
都是等边三角形.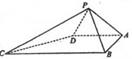
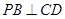 ;
;
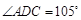 ,
,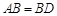 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD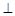 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.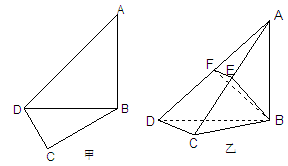
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.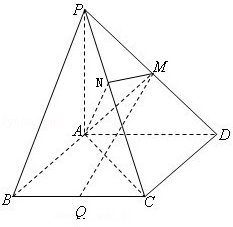
 为空间四边形
为空间四边形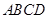 的边
的边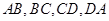 上的点,且
上的点,且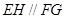 ,求证:
,求证: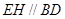 .
.
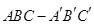 ,
,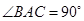 ,
,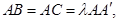 点M,N分别为
点M,N分别为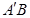 和
和 的中点.
的中点.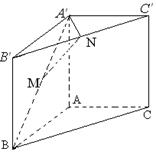
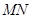 ∥平面
∥平面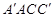 ;
;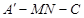 A为直二面角,求
A为直二面角,求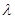 的值.
的值.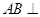 平面
平面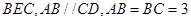 ,
, 为等边三角形.
为等边三角形.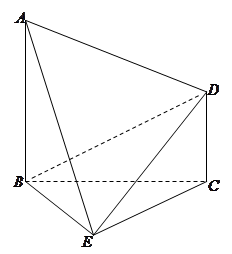
 ,求证:平面
,求证:平面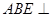 平面
平面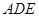 ;
;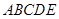 的体积为
的体积为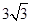 ,求此时二面角
,求此时二面角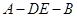 的余弦值.
的余弦值.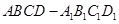 ,
,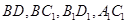 分别为各个面的对角线;
分别为各个面的对角线;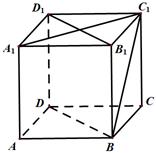
 ;
;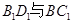 所成的角.
所成的角. 中,侧面
中,侧面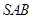 与侧面
与侧面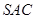 均为等边三角形,
均为等边三角形, 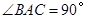 ,
,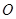 为
为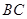 中点.
中点.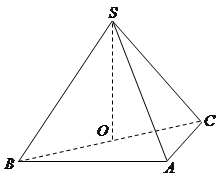
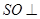 平面
平面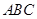 ;
;