题目内容
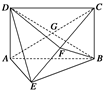
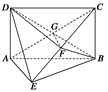
如图所示,矩形 中,
中,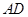 ⊥平面
⊥平面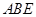 ,
,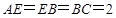 ,
,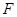 为
为 上的点,且
上的点,且 ⊥平面
⊥平面 .
.
(1)求证: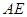 ⊥平面
⊥平面 ;
;
(2)求三棱锥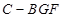 的体积.
的体积.
(1)只要证明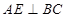 和
和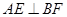 (2)
(2)
解析试题分析:解:(1)∵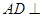 平面
平面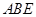 ,
,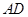 ∥
∥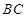 ,
,
∴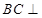 平面
平面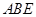 ,∴
,∴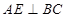 ,
,
又∵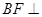 平面
平面 ,∴
,∴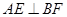 ,
,
又∵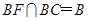 ,∴
,∴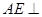 平面
平面 .
.
(2)由题意可得, 是
是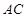 的中点,连接
的中点,连接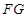 ,
,
∵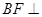 平面
平面 ,∴
,∴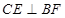 ,又∵
,又∵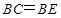 ,
,
∴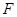 是
是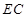 的中点,
的中点,
∴在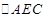 中,
中,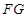 ∥
∥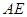 ,
,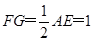 ,
,
∵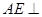 平面
平面 ,∴
,∴ 平面
平面 .
.
在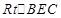 中,
中,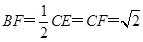 ,
,
∴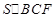 =
= ×
×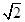 ×
×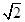 =1,
=1,
∴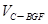 =
=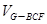 =
=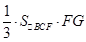 =
= .
.
考点:空间中直线与直线之间的位置关系;棱柱、棱锥、棱台的体积;直线与平面垂直的性质.
点评:本题主要考查垂直关系,利用线面垂直的定义和判定定理,进行线线垂直与线面垂直
的转化;求三棱锥体积常用的方法:换底法.

练习册系列答案
相关题目
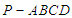 中,底面
中,底面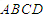 为菱形,
为菱形,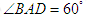 ,
,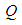 为
为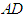 的中点。
的中点。
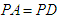 ,求证:平面
,求证:平面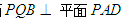 ;
;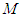 在线段
在线段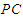 上,
上,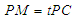 ,试确定
,试确定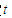 的值,使
的值,使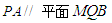 ;
;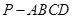 中,
中, 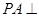 平面
平面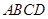 ,
,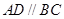 ,
,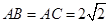 ,
,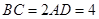 .
. 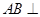 平面
平面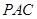 ;
;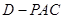 的高.
的高. 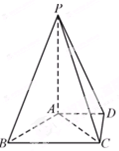
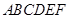 中,四边形
中,四边形 是边长为
是边长为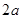 的正方形,平面
的正方形,平面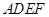 垂直于平面
垂直于平面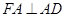 ,
,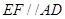 ,
,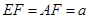 .
.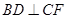 ;
;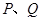 分别为棱
分别为棱 和
和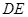 的中点,求证:
的中点,求证: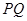 ∥平面
∥平面
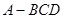 ,平面
,平面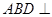 平面
平面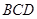 ,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC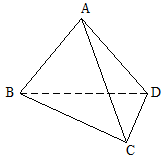
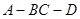 的正切值.
的正切值.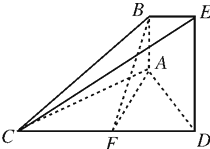
 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.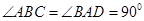 ,
,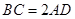 ,
,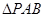 和
和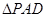 都是等边三角形.
都是等边三角形.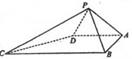
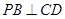 ;
;
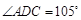 ,
,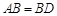 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.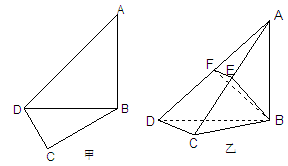
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.