题目内容
三棱锥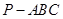 ,底面
,底面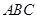 为边长为
为边长为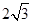 的正三角形,平面
的正三角形,平面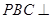 平面
平面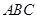 ,
,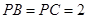 ,
,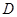 为
为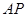 上一点,
上一点,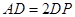 ,
,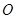 为底面三角形中心.
为底面三角形中心. 
(Ⅰ)求证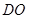 ∥面
∥面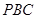 ;
;
(Ⅱ)求证: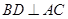 ;
;
(Ⅲ)设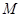 为
为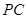 中点,求二面角
中点,求二面角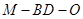 的余弦值.
的余弦值.
(Ⅰ)先证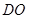 ∥
∥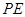 (Ⅱ)先证
(Ⅱ)先证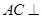 平面
平面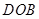 (Ⅲ)
(Ⅲ)
解析试题分析:(Ⅰ)连结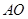 交
交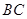 于点
于点 ,连结
,连结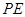 .
.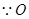 为正三角形
为正三角形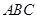 的中心,∴
的中心,∴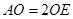 ,
,
且 为
为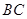 中点.又
中点.又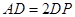 , ∴
, ∴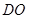 ∥
∥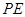 ,
, 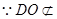 平面
平面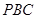 ,
,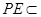 平面
平面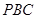
∴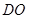 ∥面
∥面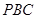 .
.
(Ⅱ)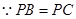 ,且
,且 为
为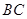 中点, ∴
中点, ∴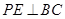 ,
,
又平面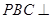 平面
平面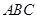 ,
,
∴ 平面
平面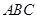 ,
,
由(Ⅰ)知,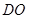 ∥
∥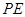 ,
,
∴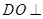 平面
平面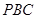 ,∴
,∴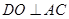
连结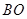 ,则
,则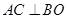 ,又
,又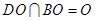 ,
,
∴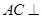 平面
平面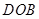 ,∴
,∴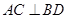 .
.
(Ⅲ)由(Ⅰ)(Ⅱ)知,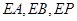 两两互相垂直,且
两两互相垂直,且 为
为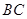 中点,所以分别以
中点,所以分别以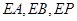 所在直线为
所在直线为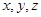 轴,建立空间直角坐标系,如图
轴,建立空间直角坐标系,如图
,则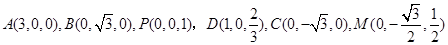
∴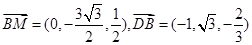
设平面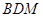 的法向量为
的法向量为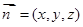 ,则
,则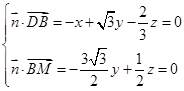 ,
,
令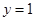 ,则
,则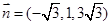 .
.
由(Ⅱ)知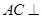 平面
平面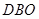 ,∴
,∴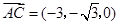 为平面
为平面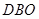 的法向量,
的法向量,
∴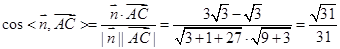 ,
,
由图可知,二面角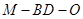 的余弦值为
的余弦值为 .
.
考点:直线与平面平行的判定;直线与平面垂直的性质;二面角的平面角及求法.
点评:本题考查直线与平面的平行的判断,在与平面垂直的性质定理的应用,二面角的求法,考查空间想象能力与计算能力,以及逻辑推理能力.

练习册系列答案
相关题目
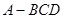 ,平面
,平面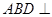 平面
平面 ,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC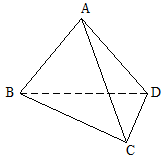
 的正切值.
的正切值. 的底面
的底面 是边长为2的菱形,
是边长为2的菱形,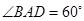 .已知
.已知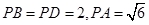 .
.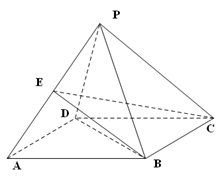
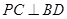
 为
为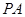 的中点,求三菱锥
的中点,求三菱锥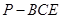 的体积.
的体积.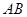 是⊙
是⊙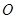 的直径,
的直径,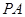 垂直于⊙
垂直于⊙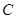 是圆周上不同于
是圆周上不同于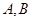 的任意一点,(1) 求证:
的任意一点,(1) 求证: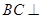 平面
平面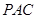 。(2) 求二面角 P-BC-A 的大小。
。(2) 求二面角 P-BC-A 的大小。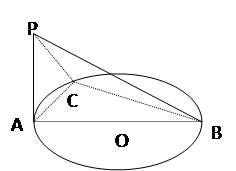
 的对棱
的对棱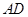 、
、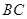 成
成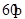 的角,且
的角,且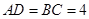 ,平行于
,平行于 、
、 、
、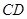 、
、 于
于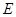 、
、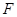 、
、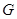 、
、 .
.
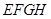 为平行四边形;
为平行四边形;
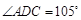 ,
,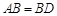 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD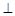 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.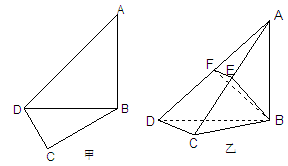
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.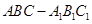 中,
中,

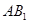 与
与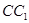 所成角的大小;
所成角的大小;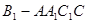 的体积。
的体积。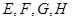 为空间四边形
为空间四边形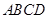 的边
的边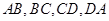 上的点,且
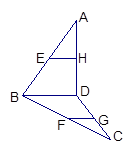
上的点,且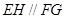 ,求证:
,求证: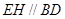 .
.
 和矩形
和矩形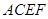 所在的平面互相垂直,
所在的平面互相垂直,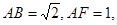
 是线段
是线段 的中点。
的中点。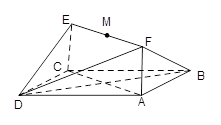
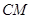 ∥平面
∥平面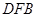
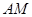 与
与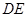 所成的角的余弦值。
所成的角的余弦值。