题目内容
有这样一个游戏项目:甲箱子里装有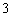 个白球,
个白球,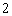 个黑球和1个红球.乙箱子里装有2 个白球,1个黑球和2个红球.这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出3个球,若摸出的6个球中白球个数比黑球多,黑球的个数比红球多,则获奖. (每次游戏结束后将球放回原箱)
个黑球和1个红球.乙箱子里装有2 个白球,1个黑球和2个红球.这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出3个球,若摸出的6个球中白球个数比黑球多,黑球的个数比红球多,则获奖. (每次游戏结束后将球放回原箱)
(Ⅰ)求在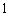 次游戏中,摸出
次游戏中,摸出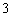 个白球,2个黑球,1个红球的概率;
个白球,2个黑球,1个红球的概率;
(Ⅱ)设在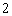 次游戏中获奖次数为
次游戏中获奖次数为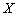 ,求数学期望
,求数学期望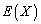 .
.
解:(Ⅰ)设“一次游戏中摸出3个白球,2个黑球,1个白球”为事件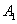
情形1: 情形2:
| 甲袋 | 乙袋 | |
| 白球 | 2 | 1 |
| 黑球 | 1 | 1 |
| 红球 | 0 | 1 |
| 甲袋 | 乙袋 | |
| 白球 | 1 | 2 |
| 黑球 | 2 | 0 |
| 红球 | 0 | 1 |
情形3:
| 甲袋 | 乙袋 | |
| 白球 | 1 | 2 |
| 黑球 | 1 | 1 |
| 红球 | 1 | 0 |
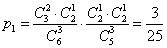
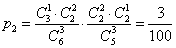

所以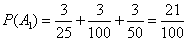
(Ⅱ)设“一次游戏中摸出4个白球,2个黑球,0个红球”为事件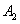
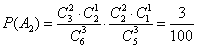
设“一次游戏中摸出5个白球,1个黑球,0个红球”为事件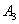
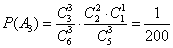
所以1次游戏获奖的概率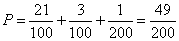 ,又
,又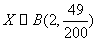
所以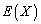 =
=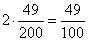 -
-

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
下面是一个2×2列联表
|
| y1 | y2 | 合计 |
| x1 | a | 21 | 73 |
| x2 | 2 | 25 | 27 |
| 合计 | b | 46 | 100 |
则表中a、b处的值分别为( )
A.94、96 B.52、50
C.52、54 D.54、52
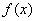 的导数
的导数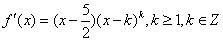 ,已知
,已知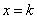 是函数
是函数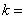 _____________;
_____________;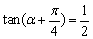 ,且
,且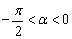 ,则
,则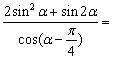
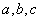 成等差数列,点
成等差数列,点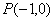 在直线
在直线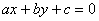 上的射影点
上的射影点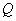 的轨迹方程为( )
的轨迹方程为( ) B.
B.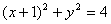
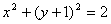 D.
D.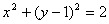
 满足
满足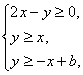 且
且 的最小值为3,则实数
的最小值为3,则实数 .
.  .小前提:已知a=-2为实数.结论:
.小前提:已知a=-2为实数.结论: .”这个结论显然错误,是因为( ).
.”这个结论显然错误,是因为( ). 中,点
中,点 ,直线
,直线 经过两点
经过两点 ,
, ,设圆
,设圆 的半径为
的半径为 ,圆心在直线
,圆心在直线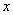 轴截得的弦长为
轴截得的弦长为 ,求圆
,求圆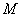 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围.